
1.函数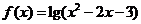 的定义域是集合
的定义域是集合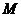 ,函数
,函数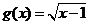 的定义域是集合
的定义域是集合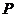 ,则
,则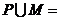 ▲ .
▲ .
2.若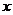 是不等式
是不等式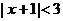 的解,则
的解,则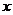 是负数的概率为 ▲ .
是负数的概率为 ▲ .
3.某医疗研究所为了检验某种血清预防感冒的作用,把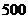 名使用血清的人与另外
名使用血清的人与另外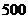 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设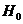 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用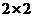 列联表计算得
列联表计算得 ,经查对临界值表知
,经查对临界值表知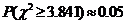 .则下列结论中,正确结论的序号是 ▲ .
.则下列结论中,正确结论的序号是 ▲ .
①有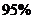 的把握认为“这种血清能起到预防感冒的作用”;
的把握认为“这种血清能起到预防感冒的作用”;
 ②若某人未使用该血清,那么他在一年中有
②若某人未使用该血清,那么他在一年中有
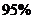 的可能性得感冒;
的可能性得感冒;
③这种血清预防感冒的有效率为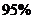 ;
;
④这种血清预防感冒的有效率为 .
.
4.一个正三棱柱的三视图如右图所示,则
这个正三棱柱的表面积是 ▲ .
5.一个均匀小正方体的6个面中,三个面上标以
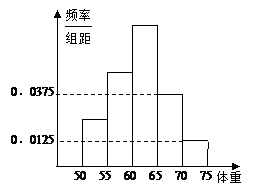 数0,其余三个面上分别标以数4,5,6.将这个小正方体抛掷2次,则向上的两个数之和等于零的概率是 ▲ .
数0,其余三个面上分别标以数4,5,6.将这个小正方体抛掷2次,则向上的两个数之和等于零的概率是 ▲ .
6.为了了解高三学生的身体状况.抽取了部分
男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12,则抽取的男生人数是 ▲ .
7.椭圆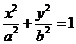 上任意一点到两焦点的距离分别为
上任意一点到两焦点的距离分别为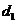 、
、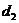 ,焦距为
,焦距为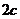 ,若
,若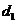 、
、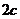 、
、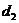 成等差数列,则椭圆的离心率为 ▲ .
成等差数列,则椭圆的离心率为 ▲ .
8.过点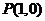 作曲线
作曲线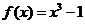 的切线,切线的方程是 ▲ .
的切线,切线的方程是 ▲ .
9.为了考察甲、乙两种小麦的长势,分别从中抽取了6株苗,测得高如下(单位: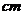 ):
):
|
甲 |
11 |
12 |
12 |
10 |
13 |
14 |
|
乙 |
12 |
13 |
9 |
13 |
12 |
13 |
由此可以估计, ▲ 种小麦长得比较整齐.
10.若方程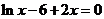 的解为
的解为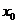 ,则不等式
,则不等式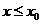 的最大整数解是 ▲ .
的最大整数解是 ▲ .
11.已知直线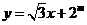 与圆
与圆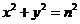 相切,其中
相切,其中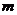 ,
,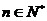 ,且
,且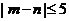 .则满足条件的有序实数对
.则满足条件的有序实数对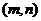 共有
▲
个.
共有
▲
个.
12.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是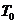 ,经过一定时间
,经过一定时间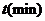 后的温度是
后的温度是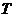 ,则
,则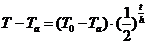 ,其中
,其中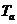 表示环境温度,
表示环境温度,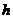 称为半衰期.现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20
称为半衰期.现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20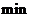 ,那么此杯咖啡从40℃降温到32℃时,还需 ▲
,那么此杯咖啡从40℃降温到32℃时,还需 ▲ 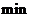 .
.
13.考察下列一组不等式:
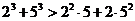 ,
,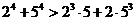 ,
,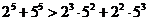 ,…….
,…….
将上述不等式在左、右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是 ▲ .
14.已知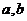 是不相等的两个正数,在
是不相等的两个正数,在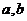 之间插入两组数:
之间插入两组数: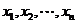 和
和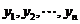 ,(
,( 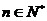 ,且
,且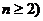 ,使得
,使得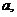
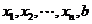 成等差数列,
成等差数列,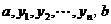 成等比数列.吴老师给出下列四个式子:①
成等比数列.吴老师给出下列四个式子:①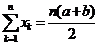 ;②
;②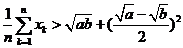 ; ③
; ③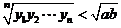 ;④
;④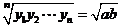 ;⑤
;⑤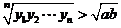 .其中一定成立的是 ▲ ;一定不成立的是 ▲ .(只需填序号).
.其中一定成立的是 ▲ ;一定不成立的是 ▲ .(只需填序号).