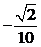1.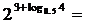 2 .
2 .
2.复数Z满足条件z+︱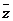 ︱
︱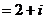 ,则z是
,则z是 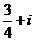 .
.
3. 若o为平行四边形ABCD的中心,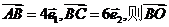 等于
等于 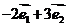 .
.
4. 若集合 ,
,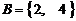 ,则“
,则“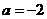 ”是“
”是“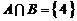 ”的 充分不必要
”的 充分不必要 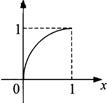 条件(填充要性).
条件(填充要性).
5. 已知定义在区间[0,1]上的函数y=f(x)图象如右图所示对满足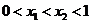 的任意
的任意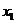 、
、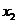 ,给出下列结论:
,给出下列结论:
(1)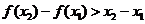 (2)
(2)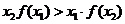
(3)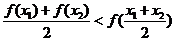
其中正确结论序号是 (2)、(3) (把所有正确结论序号都填上).
6. 已知函数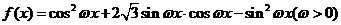 ,且
,且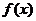 图象相邻两对称轴间的距离不小于
图象相邻两对称轴间的距离不小于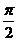 ,
,
(1)求 的取值范围;
的取值范围;
(2)设a、b、c是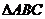 的三内角A、B、C所对的边,
的三内角A、B、C所对的边,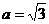 ,且当
,且当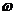 最大时
最大时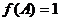 ,求
,求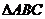 周长的取值范围。
周长的取值范围。
答案:(1)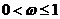 ;(2)
;(2)
7. 如图,在正方体ABCD-A1B1C1D1中,棱长为a,E为棱CC1上的的动点.
 (1)求证:A1E⊥BD;
(1)求证:A1E⊥BD;
(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD;
(3)在(2)的条件下,求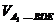 .
.
答案:(1)、(2)略
(3)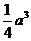
二轮复习高三数学基础题精练(2)
1.已知函数y=loga(x+1)(a>0,且a≠1)的定义域和值域都是[0,1],则a=___2_____.
2.已知向量a=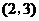 ,b=
,b=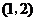 ,且(a+
,且(a+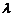 b)⊥(a-b),则
b)⊥(a-b),则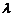 =____
=____ 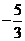 .
.
3.已知两条直线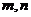 ,两个平面
,两个平面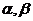 ,给出下面四个命题:
,给出下面四个命题:
①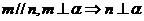 ②
② ③
③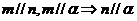 ④
④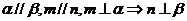 , 其中正确命题的序号是___①___④__.
, 其中正确命题的序号是___①___④__.
4.设点P是曲线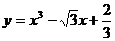 上任一点,P点处切线倾斜角为
上任一点,P点处切线倾斜角为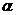 ,
,
则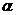 的取值范围是
的取值范围是 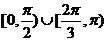 .
.
5. 图1,2,3,4分别包含1,5,13和25个互不重叠的单位正方形,按同样的方式构造图形,则第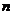 个图包含_____
个图包含_____  ___个互不重叠的单位正方形.
___个互不重叠的单位正方形.

6. 已知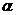 为锐角,且
为锐角,且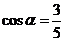 .
.
(Ⅰ)求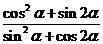 的值; (Ⅱ)求
的值; (Ⅱ)求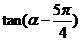 的值.
的值.
答案:(1) 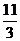 (2)
(2)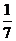
7. 已知曲线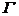 上任意一点
上任意一点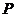 到两个定点
到两个定点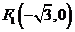 和
和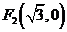 的距离之和为4.
的距离之和为4.
(1)求曲线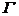 的方程;
的方程;
(2)设过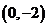 的直线
的直线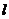 与曲线
与曲线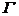 交于
交于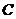 、
、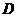 两点,且
两点,且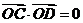 (
(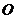 为坐标原点),求直线
为坐标原点),求直线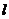 的方程.
的方程.
答案: (1)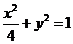 (2)
(2)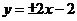
二轮复习高三数学基础题精练(3)
1.
已知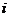 是虚数单位,则复数
是虚数单位,则复数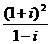 等于
等于 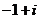 .
.
2. 函数y=在(-1,+∞)上单调递减,则实数a的取值范围是________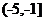 ______.
______.
3. △ABC的三内角A、B、C所对边的长分别为a、b、c,设向量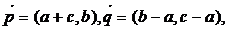
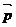 ∥
∥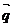 ,则角C的大小为
900 .
,则角C的大小为
900 .
4.
已知圆C: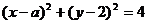 及直线
及直线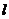 :
: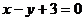 ,当直线
,当直线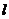 被C截得的弦长为
被C截得的弦长为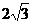 时,则
时,则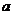 等于
等于
 .
.
5. 设有两个命题:(1)关于x的不等式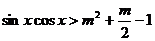 的解集是R;(2)函数
的解集是R;(2)函数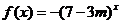 是减函数.若这两个命题都是真命题,则m的取值范围是
是减函数.若这两个命题都是真命题,则m的取值范围是 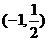 .
.
6. 在 中,已知内角
中,已知内角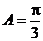 ,边
,边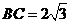 .设内角
.设内角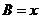 ,周长为
,周长为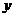 ,
,
(Ⅰ)求函数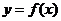 的解析式和定义域;(Ⅱ)求
的解析式和定义域;(Ⅱ)求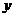 的最大值.
的最大值.
答案:(I)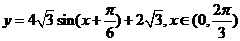
(II)当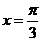 时,
时,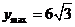 。
。
7.已知数列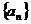 中,
中, ,
,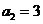 ,其前
,其前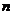 项和
项和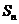 满足
满足
 (
( ,
,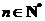 ).
).
(I)求数列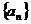 的通项公式;
(II) 求数列
的通项公式;
(II) 求数列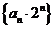 的前n项的和.
的前n项的和.
答案:(I)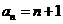
(II)数列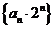 的前n项的和为
的前n项的和为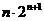
二轮复习高三数学基础题精练(4)
1. 已知等比数列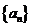 的前三项依次为
的前三项依次为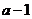 ,
,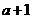 ,
,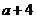 ,则
,则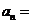
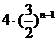 .
.
2. 下图是一个物体的三视图,根据图中尺寸,它的体积为
8 .
下图是一个物体的三视图,根据图中尺寸,它的体积为
8 .
3.已知直线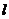 、
、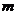 ,平面
,平面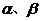 ,则①若
,则①若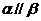 ,
,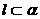 ,则
,则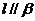 , ②若
, ②若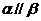 ,
,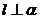 ,则
,则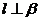 ,③若
,③若 ,
, ,则
,则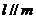 , ④
, ④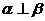 ,
,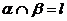 ,
,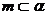 ,
,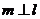 ,则
,则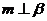 ,
其中假命题是
③ .
,
其中假命题是
③ .
4. 设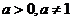 ,函数
,函数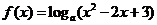 有最小值,则不等式
有最小值,则不等式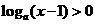 的解集为
的解集为 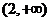 .
.
5.已知函数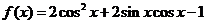 的图象与
的图象与 的图象在
的图象在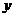 轴的右侧交点按从横坐标由小到大的顺序记为
轴的右侧交点按从横坐标由小到大的顺序记为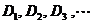 ,则
,则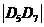 =
= 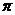 .
.
6. 二次函数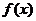 满足
满足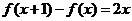 ,且
,且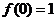 .
.
(1)求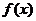 的解析式; (2)当
的解析式; (2)当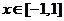 时,
时,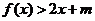 恒成立,求实数
恒成立,求实数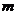 的取值范围.
的取值范围.
答案:(1)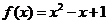 (2)
(2)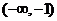
7.
已知数列{an}的前n项为和Sn,点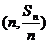 在直线
在直线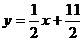 上,数列{bn}满足
上,数列{bn}满足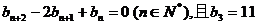 ,前9项和为153,
求数列{an}、{bn}的通项公式.
,前9项和为153,
求数列{an}、{bn}的通项公式.
答案: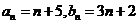
二轮复习高三数学基础题精练(5)
1. 如果复数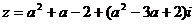 为纯虚数,那么实数
为纯虚数,那么实数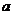 的值为 -2 .
的值为 -2 .
2. 用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
用单位立方块搭一个几何体,使它的主视图和俯视图如右图所示,
则它的体积的最小值与最大值分别为 10 、 16 .
3. 下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 85、
1. 4 .
下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 85、
1. 4 .
4. 下图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,
数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影
 部分的面积为 4.6
.
部分的面积为 4.6
.
5.若实数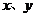 满足条件
满足条件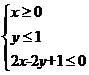 ,则目标函数
,则目标函数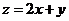 的最大值为___ 2
__ .
的最大值为___ 2
__ .
6.已知函数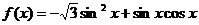
(I)求函数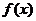 的最小正周期; (II)求函数
的最小正周期; (II)求函数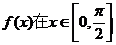 的值域.
的值域.
答案:(I)最小正周期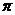 (II)
(II)
7.已知圆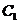 :
: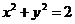 和圆
和圆 ,直线
,直线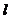 与圆
与圆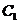 相切于点
相切于点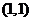 ;圆
;圆 的圆心在射线
的圆心在射线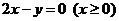 上,圆
上,圆 过原点,且被直线
过原点,且被直线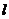 截得的弦长为
截得的弦长为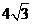 .
.
(Ⅰ)求直线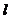 的方程; (Ⅱ)求圆
的方程; (Ⅱ)求圆 的方程.
的方程.
答案:(Ⅰ)直线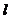 的方程:x+y=2; (Ⅱ)圆
的方程:x+y=2; (Ⅱ)圆 的方程:
的方程: 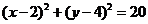 .
.
二轮复习高三数学基础题精练(6)
1.函数f (x)= x3+ax+1在(-∞,-1)上为增函数,在(-1,1)上为减函数,则f (1)的值为 .
2. 设复数z=lg(m2-2m-2)+(m2+3m+2)i是纯虚数,则实数m的值为 3 .
3. 若数列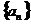 中,
中,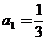 ,且对任意的正整数
,且对任意的正整数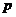 、
、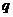 都有
都有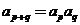 ,则
,则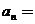
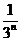 .
.
4. 若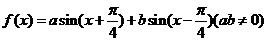 是偶函数,则点(
是偶函数,则点(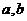 )所在的直线方程为
)所在的直线方程为
x+y=0 .
5. 在平面直角坐标系xoy中,点P(x,y)满足不等式组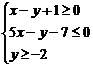 ,OX轴上正向单位向量为
,OX轴上正向单位向量为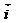 ,则向量
,则向量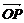 在向量
在向量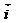 上的投影的取值范围为
[0,2] .
上的投影的取值范围为
[0,2] .
6. 向量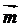 = (1,1),
= (1,1),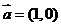 且
且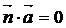 ,
,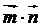 = - 1.
= - 1.
(I)求向量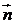 及向量
及向量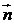 与向量
与向量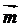 的夹角;
的夹角;
(II)设向量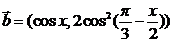 ,其中
,其中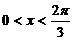 ,试求
,试求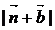 的取值范围.
的取值范围.
答案:(I)向量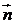 =(0,-1),向量
=(0,-1),向量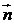 与向量
与向量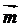 的夹角为1800
的夹角为1800
(II) 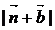 的取值范围是
的取值范围是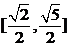 .
.
7. 设A、B为圆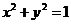 上两点,O为坐标原点(A、O、B不共线)
上两点,O为坐标原点(A、O、B不共线)
(Ⅰ)求证: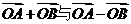 垂直;
垂直;
(Ⅱ)当 时.求
时.求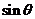 的值.
的值.
答案:(Ⅰ)略
(Ⅱ)