
1.()在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A.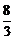 B.
B.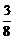 C.
C.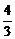 D.
D.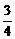
2.()在直二面角α-l-β中,直线a α,直线b
α,直线b β,a、b与l斜交,则( )
β,a、b与l斜交,则( )
A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b
C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b
3.()设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z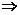 X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号).
①X、Y、Z是直线 ②X、Y是直线,Z是平面 ③Z是直线,X、Y是平面 ④X、Y、Z是平面
4.()设a,b是异面直线,下列命题正确的是_________.
①过不在a、b上的一点P一定可以作一条直线和a、b都相交
②过不在a、b上的一点P一定可以作一个平面和a、b都垂直
③过a一定可以作一个平面与b垂直
④过a一定可以作一个平面与b平行
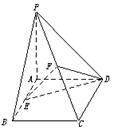
5.()如图,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(1)求证:CD⊥PD;
(2)求证:EF∥平面PAD;
(3)当平面PCD与平面ABCD成多大角时,直线EF⊥平面PCD?
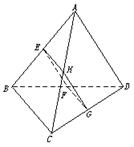
6.()如图,在正三棱锥A-BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
(1)判定四边形EFGH的形状,并说明理由.
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFGH,请给出证明.
7.()如图,正三棱柱ABC-A1B1C1的各棱长都相等,D、E分别是CC1和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
(1)若M为AB中点,求证:BB1∥平面EFM;
(2)求证:EF⊥BC;
(3)求二面角A1-B1D-C1的大小.
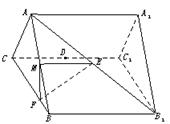
8.()如图,已知平行六面体ABCD-A1B1C1D1的底面是菱形且∠C1CB=
∠C1CD=∠BCD=60°,
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=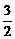 ,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
(3)当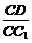 的值为多少时,可使A1C⊥面C1BD?
的值为多少时,可使A1C⊥面C1BD?
难点26 垂直与平行 垂直与平行是高考的重点内容之一,考查内容灵活多样.本节主要帮助考生深刻理解线面平行与垂直、面面平行与垂直的判定与性质,并能利用它们解决一些问题. ●难点磁场 ()已知斜三棱柱ABC-A1B1C1中,A1C1=B1C1=2,D、D1分别是AB、A1B1的中点,平面A1ABB1⊥平面A1B1C1,异面直线AB1和C1B互相垂直. (1)求证:AB1⊥C1D1; (2)求证:AB1⊥面A1CD; (3)若AB1=3,求直线AC与平面A1CD所成的角. ●案例探究 [例参考答案
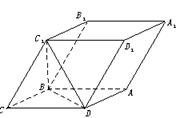
参考答案
难点磁场
1.(1)证明:∵A1C1=B1C1,D1是A1B1的中点,∴C1D1⊥A1B1于D1,
又∵平面A1ABB1⊥平面A1B1C1,∴C1D1⊥平面A1B1BA,
而AB1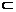 平面A1ABB1,∴AB1⊥C1D1.
平面A1ABB1,∴AB1⊥C1D1.
(2)证明:连结D1D,∵D是AB中点,∴DD1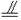 CC1,∴C1D1∥CD,由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,由三垂线定理得BD1⊥AB1,
CC1,∴C1D1∥CD,由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,由三垂线定理得BD1⊥AB1,
又∵A1D∥D1B,∴AB1⊥A1D而CD∩A1D=D,∴AB1⊥平面A1CD.
(3)解:由(2)AB1⊥平面A1CD于O,连结CO1得∠ACO为直线AC与平面A1CD所成的角,∵AB1=3,AC=A1C1=2,∴AO=1,∴sinOCA= ,
,
∴∠OCA=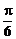 .
.
歼灭难点训练
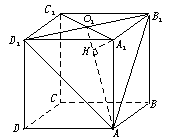
一、1.解析:如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,故平面AA1O1⊥AB1D1,交线为AO1,在面AA1O1内过A1作A1H⊥AO1于H,则易知A1H长即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=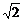 ,AO1=3
,AO1=3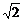 ,由A1O1.A1A=h.AO1,可得A1H=
,由A1O1.A1A=h.AO1,可得A1H=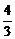 .
.
答案:C
2.解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,
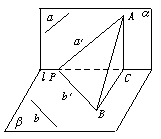
∴△APB为直角三角形,故∠APB为锐角.
答案:C
二、3.解析:①是假命题,直线X、Y、Z位于正方体的三条共点棱时为反例,②③是真命题,④是假命题,平面X、Y、Z位于正方体的三个共点侧面时为反例.
答案:②③
4.④
三、5.证明:(1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD内的射影,
∵CD 平面ABCD且CD⊥AD,∴CD⊥PD.
平面ABCD且CD⊥AD,∴CD⊥PD.
(2)取CD中点G,连EG、FG,
∵E、F分别是AB、PC的中点,∴EG∥AD,FG∥PD
∴平面EFG∥平面PAD,故EF∥平面PAD
(3)解:当平面PCD与平面ABCD成45°角时,直线EF⊥面PCD
证明:G为CD中点,则EG⊥CD,由(1)知FG⊥CD,故∠EGF为平面PCD与平面ABCD所成二面角的平面角.即∠EGF=45°,从而得∠ADP=45°,AD=AP
由Rt△PAE≌Rt△CBE,得PE=CE
又F是PC的中点,∴EF⊥PC,由CD⊥EG,CD⊥FG,得CD⊥平面EFG,CD⊥EF即EF⊥CD,故EF⊥平面PCD.
6.(1)证明:
同理EF∥FG,∴EFGH是平行四边形
∵A-BCD是正三棱锥,∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC,∴AD⊥BC,
∴HG⊥EH,四边形EFGH是矩形.
(2)作CP⊥AD于P点,连结BP,∵AD⊥BC,∴AD⊥面BCP
∵HG∥AD,∴HG⊥面BCP,HG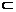 面EFGH.面BCP⊥面EFGH,
面EFGH.面BCP⊥面EFGH,
在Rt△APC中,∠CAP=30°,AC=a,∴AP=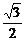 a.
a.
7.(1)证明:连结EM、MF,∵M、E分别是正三棱柱的棱AB和AB1的中点,
∴BB1∥ME,又BB1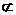 平面EFM,∴BB1∥平面EFM.
平面EFM,∴BB1∥平面EFM.
(2)证明:取BC的中点N,连结AN由正三棱柱得:AN⊥BC,
又BF∶FC=1∶3,∴F是BN的中点,故MF∥AN,
∴MF⊥BC,而BC⊥BB1,BB1∥ME.
∴ME⊥BC,由于MF∩ME=M,∴BC⊥平面EFM,
又EF平面EFM,∴BC⊥EF.
(3)解:取B1C1的中点O,连结A1O知,A1O⊥面BCC1B1,由点O作B1D的垂线OQ,垂足为Q,连结A1Q,由三垂线定理,A1Q⊥B1D,故∠A1QD为二面角A1-B1D-C的平面角,易得∠A1QO=arctan .
.
8.(1)证明:连结A1C1、AC,AC和BD交于点O,连结C1O,
∵四边形ABCD是菱形,∴AC⊥BD,BC=CD
又∵∠BCC1=∠DCC1,C1C是公共边,∴△C1BC≌△C1DC,∴C1B=C1D
∵DO=OB,∴C1O⊥BD,但AC⊥BD,AC∩C1O=O
∴BD⊥平面AC1,又C1C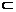 平面AC1,∴C1C⊥BD.
平面AC1,∴C1C⊥BD.
(2)解:由(1)知AC⊥BD,C1O⊥BD,∴∠C1OC是二面角α-BD-β的平面角.
在△C1BC中,BC=2,C1C=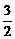 ,∠BCC1=60°,∴C1B2=22+(
,∠BCC1=60°,∴C1B2=22+(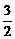 )2-2×2×
)2-2×2×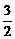 ×cos60°=
×cos60°=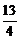 .
.
∵∠OCB=30°,∴OB=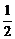 ,BC=1,C1O=
,BC=1,C1O=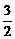 ,即C1O=C1C.
,即C1O=C1C.
作C1H⊥OC,垂足为H,则H是OC中点且OH=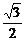 ,∴cosC1OC=
,∴cosC1OC=
(3)解:由(1)知BD⊥平面AC1,∵A1O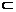 平面AC1,∴BD⊥A1C,当
平面AC1,∴BD⊥A1C,当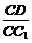 =1时,平行六面体的六个面是全等的菱形,同理可证BC1⊥A1C,又∵BD∩BC1=B,∴A1C⊥平面C1BD.
=1时,平行六面体的六个面是全等的菱形,同理可证BC1⊥A1C,又∵BD∩BC1=B,∴A1C⊥平面C1BD.