1.()某商场对顾客实行购物优惠活动，规定一次购物付款总额：①如果不超过200元，则不予优惠，②如果超过200元但不超过500元，则按标价给予9折优惠，③如果超过500元，其500元按②条给予优惠，超过500元的部分给予7折优惠.某人两次去购物，分别付款168元和423元，假设他一次购买上述同样的商品，则应付款( )
A.413.7元 B.513.7元 C.546.6元 D.548.7元
2.()某体育彩票规定：从01到36共36个号码中抽出7个号码为一注，每注2元.某人想先选定吉利号18，然后再从01到17中选3个连续的号，从19到29中选2个连续的号，从30到36中选1个号组成一注，则此人把这种要求的号买全，至少要花( )
A.1050元 B.1052元 C.2100元 D.2102元
3.
()一个球从100米高处自由落下，每次着地后又跳回到原高度的一半再落下，当它最后静止在地面上时，共经过了 米.
4.()有一广告气球直径为6米，放在公司大楼上空(如图)，当某行人在A地观测气球时，其中心仰角为∠BAC=30°，并测得气球的视角β=2°，若θ很小时，可取sinθ=θ，试估计气球的高BC的值约为 米.
5.()运输一批海鲜，可在汽车、火车、飞机三种运输工具中选择，它们的速度分别为v千米/小时、2v千米/小时、10v千米/小时，每千米的运费分别为a元、b元、c元.且b＜a＜c,又这批海鲜在运输过程中的损耗为m元/小时，若使用三种运输工具分别运输时各自的总费用(运费与损耗之和)互不相等.试确定使用哪种运输工具总费用最省.(题中字母均为正的已知量)
6.()已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24，单位小时)的函数，记作y=f(t)，下表是某日各时的浪高数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1.5 |
1.0 |
0.5 |
1.0 |
1.49 |
1 |
0.51 |
0.99 |
1.5 |
经长期观测y=f(t)的曲线可近似地看成函数y=Acosωt+b.
(1)根据以上数据，求出函数y=Acosωt+b的最小正周期T，振幅A及函数表达式；
(2)依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据(1)的结论，判断一天内的上午8：00至晚上20：00之间，有多少时间可供冲浪者进行运动.
7.()某外商到一开放区投资72万美元建起一座蔬菜加工厂，第一年各种经费12万美元，以后每年增加4万美元，每年销售蔬菜收入50万美元.
(1)若扣除投资及各种经费，则从第几年开始获取纯利润？
(2)若干年后，外商为开发新项目，有两种处理方案：①年平均利润最大时以48万美元出售该厂；②纯利润总和最大时，以16万元出售该厂，问哪种方案最合算？
8.()某厂使用两种零件A、B装配两种产品P、Q，该厂的生产能力是月产P产品最多有2500件，月产Q产品最多有1200件；而且组装一件P产品要4个A、2个B，组装一件Q产品要6个A、8个B，该厂在某个月能用的A零件最多14000个；B零件最多12000个.已知P产品每件利润1000元，Q产品每件2000元，欲使月利润最大，需要组装P、Q产品各多少件？最大利润多少万元.
08高考数学应用性问题 数学应用题是指利用数学知识解决其他领域中的问题.高考对应用题的考查已逐步成熟，大体是三道左右的小题和一道大题，注重问题及方法的新颖性，提高了适应陌生情境的能力要求. ●难点磁场 1.()一只小船以10 m/s的速度由南向北匀速驶过湖面，在离湖面高20米的桥上，一辆汽车由西向东以20 m/s的速度前进(如图)，现在小船在水平P点以南的40米处，汽车在桥上以西Q点30米处(其中PQ⊥水面)，则小船与汽车间的最短距离为 .(不考虑汽车与小船本身的大小). 2.()小参考答案
参 考 答 案
●难点磁场
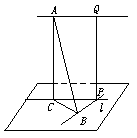1.解析：设经过时间t汽车在A点，船在B点，(如图)，则AQ=30–20t,BP=40–10t,PQ=20,且有AQ⊥BP，PQ⊥AQ，PQ⊥PB，设小船所在平面为α,AQ,QP确定平面为β,记α∩β=l,由AQ∥α,AQ
β得AQ∥l,又AQ⊥PQ，得PQ⊥l,又PQ⊥PB，及l∩PB=P得PQ⊥α.作AC∥PQ，则AC⊥α.连CB，则AC⊥CB，进而AQ⊥BP，CP∥AQ得CP⊥BP，∴AB2=AC2+BC2=PQ2+PB2+PC2=202+(40–10t)2+(30–20t)2=100［5(t–2)2+9］,t=2时AB最短，最短距离为
30 m.
答案：30 m
2.解析：按以下工序操作所需时间最少，①、④(并在此时完成②、③、⑤)所用时间为2+10+3=15分钟.
答案：15
3.解：依题意，G(x)=x+2,设利润函数为f(x),则
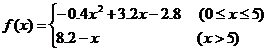
(1)要使工厂有赢利，则有f(x)>0.
当0≤x≤5时，有–0.4x2+3.2x–2.8>0,得1<x<7,∴1<x≤5.
当x>5时，有8.2–x>0,得x<8.2,∴5<x<8.2.
综上，要使工厂赢利，应满足1<x<8.2.即产品应控制在大于100台小于820台的范围内.
(2)0≤x≤5时，f(x)=–0.4(x–4)2+3.6
故当x=4时，f(x)有最大值3.6.
而当x>5时f(x)<8.2–5=3.2
所以当工厂生产400台产品时，赢利最大，此时只须求x=4时，每台产品售价为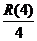
=2.4(万元/百台)=240(元/台).
●歼灭难点训练
一、1.解析：此人购买的商品原价为168+423÷90%=638元，若一次购买同样商品应付款为500×90%+(638–500)×70%=450+96.5=546.6元.
答案：C
2.解析：从01到17中选连续3个号有15种方法，从19到29中选连续2个号有10种选法，从30到36中选1个有7种选法，故购买注数为1050注至少花1050×2=2100元.
答案：C
二、3.解析：小球经过的路程为：
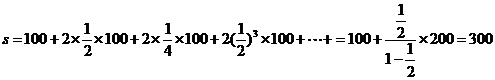m.
答案：300
4.提示：sin2°=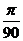
答案：86 m
三、5.解：设运输路程为S(千米)，使用汽车、火车、飞机三种运输工具运输时各自的总费用分别为y1(元)、y2(元)、y3(元).则由题意，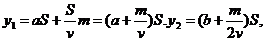
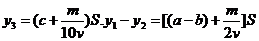,由a>b,各字母均为正值，所以y1–y2>0，即y2<y1.由y3–y2=［(c–b)–
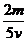］S.令y3–y2>0,由c>b及每字母都是正值，得c>b+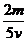.所以，当c>b+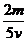时y2<y3,由y2<y1即y2最小，当b<a<c<b+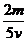时，y3<y2<y1,y3最小.
6.解：(1)由表中数据，知T=12，ω=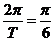
.
由t=0,y=1.5得A+b=1.5.
由t=3,y=1.0,得b=1.0.所以，A=0.5,b=1.振幅A=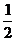
，
∴y=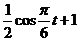
(2)由题意知，当y>1时，才可对冲浪者开放.∴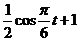>1,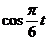 
>0.∴2kπ–
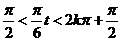,即有12k–3<t<13k+3.
由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24.
∴在规定时间内有6个小时可供冲浪者运动即上午9：00至下午15：00.
7.解：由题意知，每年的经费是以12为首项，4为公差的等差数列，设纯利润与年数的关系为f(n),则f(n)=50n–［12n+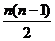
×4］–72=–2n2+40n–72
(1)获纯利润就是要求f(n)>0,∴–2n2+40n–72>0，解得2<n<18.由n∈N知从第三年开始获利.
(2)①年平均利润=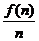
=40–2(n+
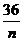)≤16.当且仅当n=6时取等号.故此方案先获利6×16+48=144(万美元)，此时n=6,②f(n)=–2(n–10)2+128.
当n=10时，f(n)|max=128.故第②种方案共获利128+16=144(万美元).
故比较两种方案，获利都是144万美元，但第①种方案只需6年，而第②种方案需10年，故选择第①种方案.
8.解：设分别生产P、Q产品x件、y件，则有
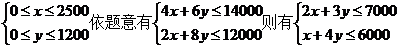
设利润S=1000x+2000y=1000(x+2y)
要使利润S最大，只需求x+2y的最大值.
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
∴
∴
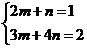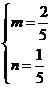
有x+2y=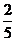
(2x+3y)+
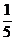(x+4y)≤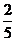×7000+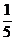×6000.
当且仅当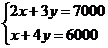
解得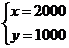
时取等号，此时最大利润Smax=1000(x+2y)
=4000000=400(万元).
另外此题可运用“线性规划模型”解决.