1.设ABCD是空间四边形,E,F分别是AB,CD的中点,则 满足( )
满足( )
A 共线 B 共面 C 不共面 D 可作为空间基向量
2.在正方体ABCD-A B
B C
C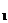 D
D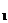 ,O是底面ABCD的中心,M、N分别是棱DD
,O是底面ABCD的中心,M、N分别是棱DD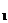 、D
、D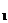 C
C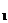 的中点,则直线OM( )
的中点,则直线OM( )
A 是AC和MN的公垂线 B 垂直于AC但不垂直于MN
C 垂直于MN,但不垂直于AC D 与AC、MN都不垂直
3.已知平面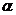 ∥平面
∥平面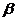 ,直线L
,直线L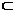 平面
平面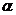 ,点P
,点P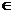 直线L,平面
直线L,平面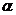 、
、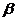 间的距离为8,则在
间的距离为8,则在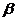 内到点P的距离为10,且到L的距离为9的点的轨迹是( )
内到点P的距离为10,且到L的距离为9的点的轨迹是( )
A 一个圆 B 四个点 C 两条直线 D 两个点
4.正方体ABCD-A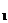 B
B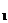 C
C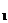 D
D 中,点P在侧面BCC
中,点P在侧面BCC B
B 及其边界上运动,并且总保持AP⊥BD
及其边界上运动,并且总保持AP⊥BD ,则动点P的轨迹(
)
,则动点P的轨迹(
)
A 线段B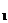 C
B BB
C
B BB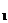 的中点与CC
的中点与CC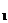 中点连成的线段
中点连成的线段
C 线段BC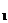 D CB中点与B
D CB中点与B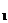 C
C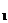 中点连成的线段
中点连成的线段
5. 下列命题中:
①
若向量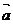 、
、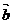 与空间任意向量不能构成基底,则
与空间任意向量不能构成基底,则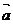 ∥
∥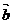 。
。
②
若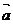 ∥
∥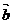 ,
,
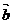 ∥
∥ ,则
,则 ∥
∥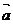 .
.
③
若 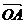 、
、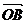 、
、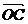 是空间一个基底,且
是空间一个基底,且 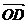 =
=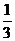
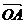 +
+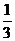
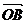 +
+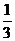
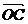 ,则A、B、C、D四点共面。
,则A、B、C、D四点共面。
④
若向量 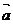 +
+ 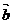 ,
,
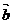 +
+  ,
,
 +
+ 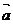 是空间一个基底,则
是空间一个基底,则 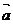 、
、 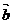 、
、  也是空间的一个基底。其中正确的命题有( )个。
也是空间的一个基底。其中正确的命题有( )个。
A 1 B 2 C 3 D 4
6.给出下列命题:①分别和两条异面直线AB、CD同时相交的两条直线AC、BD一定是异面直线②同时与两条异面直线垂直的两直线不一定平行③斜线b在面α内的射影为c,直线a⊥c,则a⊥b④有三个角为直角的四边形是矩形,其中真命题是( )
7.已知一个正四面体和一个正八面体的棱长相等,把它们拼接起来,使一个表面重合,所得多面体的面数有( )
A、7 B、8 C、9 D、10
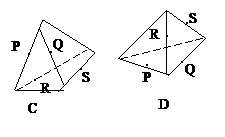
8.下列正方体或正四面体中,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是( )

9. a和b为异面直线,则过a与b垂直的平面( )
A、有且只有一个 B、一个面或无数个
C、可能不存在 D、可能有无数个
10.给出下列四个命题:
(1)各侧面在都是正方形的棱柱一定是正棱柱.
(2)若一个简单多面体的各顶点都有3条棱,则其顶点数V、面数F满足的关系式为2F-V=4.
(3)若直线l⊥平面α,l∥平面β,则α⊥β.
(4)命题“异面直线a、b不垂直,则过a的任一平面与b都不垂直”的否定.
其中,正确的命题是 ( )
A.(2)(3) B.(1)(4) C.(1)(2)(3) D.(2)(3)(4)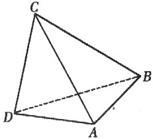
11.如图,△ABC是简易遮阳棚,A,B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为了使遮阴影面ABD面积最大,遮阳棚ABC与地面所成的角应为( )
A.75° B.60° C.50° D.45°
12.一直线与直二面角的两个面所成的角分别为α,β,则α+β满足( )
A、α+β<900 B、α+β≤900 C、α+β>900 D、α+β≥900
。
13.在正方体AC1中,过它的任意两条棱作平面,则能作得与A1B成300角的平面的个数为( )
A、2个 B、4个 C、6个 D、8个
14.△ABC的BC边上的高线为AD,BD=a,CD=b,将△ABC沿AD折成大小为θ的二面角B-AD-C,若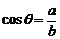 ,则三棱锥A-BCD的侧面三角形ABC是( )
,则三棱锥A-BCD的侧面三角形ABC是( )
A、锐角三角形 B、钝角三角形
C、直角三角形 D、形状与a、b的值有关的三角形
15.设a,b,c表示三条直线,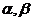 表示两个平面,则下列命题中逆命题不成立的是( )。
表示两个平面,则下列命题中逆命题不成立的是( )。
A.
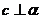 ,若
,若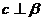 ,则
,则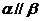
B.
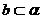 ,
,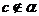 ,若
,若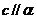 ,则
,则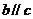
C.
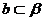 ,若
,若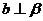 ,则
,则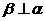
D.
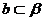 ,
,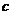 是
是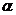 在
在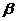 内的射影,若
内的射影,若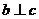 ,则
,则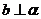
16. 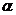 和
和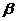 是两个不重合的平面,在下列条件中可判定平面
是两个不重合的平面,在下列条件中可判定平面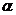 和
和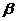 平行的是( )。
平行的是( )。
A.
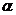 和
和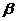 都垂直于平面
都垂直于平面
B.
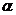 内不共线的三点到
内不共线的三点到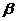 的距离相等
的距离相等
C.
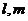 是
是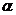 平面内的直线且
平面内的直线且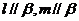
D.
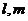 是两条异面直线且
是两条异面直线且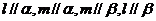
17.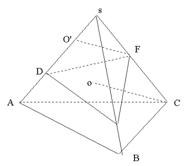 一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的(
)
一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞D、E、F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的(
)
A.
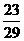
B.
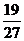
C.
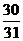 D.
D.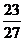
18.球的半径是R,距球心4R处有一光源,光源能照到的地方用平面去截取,则截面的最大面积是( )。
A.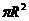 B.
B.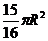 C.
C. D.
D.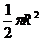
19.
|
|
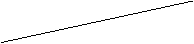 已知AB是异面直线的公垂线段,AB=2,且
已知AB是异面直线的公垂线段,AB=2,且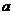 与
与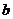 成
成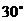 角,在直线
角,在直线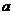 上取AP=4,则点P到直线
上取AP=4,则点P到直线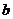 的距离是(
)。
的距离是(
)。
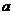
E.
|


F. 4
G.
|

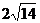
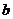
H.
 或
或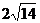
20.若平面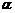 外的直线
外的直线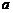 与平面
与平面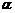 所成的角为
所成的角为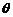 ,则
,则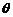 的取值范围是
( )
的取值范围是
( )
(A)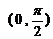 (B)
(B)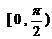 (C)
(C) (D)
(D)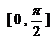
21.如果a,b是异面直线,P是不在a,b上的任意一点,下列四个结论:(1)过P一定可作直线L与a , b都相交;(2)过P一定可作直线L与a , b都垂直;(3)过P一定可作平面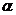 与a , b都平行;(4)过P一定可作直线L与a , b都平行,其中正确的结论有( )
与a , b都平行;(4)过P一定可作直线L与a , b都平行,其中正确的结论有( )
A、0个 B、1个 C、2个 D、3个
22.空间四边形中,互相垂直的边最多有( )
A、1对 B、2对 C、3对 D、4对
23.底面是正三角形,且每个侧面是等腰三角形的三棱锥是
A、一定是正三棱锥 B、一定是正四面体 C、不是斜三棱锥 D、可能是斜三棱锥
24.给出下列四个命题:
(1) 各侧面都是正方形的棱柱一定是正棱柱
(2) 若一个简单多面体的各顶点都有三条棱,则其顶点数V,面数F满足的关系式为2F-V=4
(3) 若直线L⊥平面α,L∥平面β,则α⊥β
(4) 命题“异面直线a,b不垂直,则过a的任一平面和b都不垂直”的否定,其中,正确的命题是 ( )
A、(2)(3) B、(1)(4) C、(1)(2)(3) D、(2)(3)(4)
二填空题:
1. 有一棱长为a的正方体骨架,其内放置一气球,使其充气且尽可能地大(仍保持为球的形状),则气球表面积的最大值为__________.
2.
一个广告气球某一时刻被一束平行光线投射到水平地面上的影子是一个椭圆,椭圆的离心率为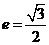 ,则该时刻这平行光线对于水平平面的入射角为________。
,则该时刻这平行光线对于水平平面的入射角为________。
3.
已知正三棱柱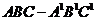 底面边长是10,高是12,过底面一边AB,作与底面ABC成
底面边长是10,高是12,过底面一边AB,作与底面ABC成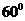 角的截面面积是___________________。
角的截面面积是___________________。
4.
平面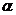 外有两点A,B,它们与平面
外有两点A,B,它们与平面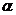 的距离分别为a,b,线段AB上有一点P,且AP:PB=m:n,则点P到平面
的距离分别为a,b,线段AB上有一点P,且AP:PB=m:n,则点P到平面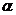 的距离为_________________.
的距离为_________________.
5.
点AB到平面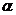 距离距离分别为12,20,若斜线AB与
距离距离分别为12,20,若斜线AB与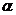 成
成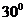 的角,则AB的长等于_____.
的角,则AB的长等于_____.
6.与空间四边形ABCD四个顶点距离相等的平面共有______个。
7.在棱长为1的正方体ABCD--A1B1C1D1中,若G、E分别为BB1,C1D1的中点,点F是正方形ADD1A1的中心,则四边形BGEF在正方体六个面上的射影图形面积的最大值为________。
8.△ABC是简易遮阳板,A、B是南北方向上两个定点,正东方向射出的太阳光线与地面成40°角,为使遮阴的阴影面ABD面积最大,遮阳板ABC与地面所成角应为_________。
9.平面α与平面β相交成锐角θ,面α内一个圆在面β上的射影是离心率为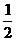 的椭圆,则角θ等于_______。
的椭圆,则角θ等于_______。
错误原因:分析不出哪些线段射影长不变,哪些线段射影长改变。
10把半径为r的四只小球全部放入一个大球内,则大球半径的最小值为__________。
11.AB垂直于 所在的平面,
所在的平面, ,当
,当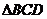 的面积最大时,点A到直线CD的距离为
。正确答案:
的面积最大时,点A到直线CD的距离为
。正确答案: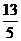
12.在平面角为600的二面角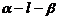 内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱l的距离为____________
内有一点P,P到α、β的距离分别为PC=2cm,PD=3cm,则P到棱l的距离为____________
答案: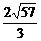 cm
cm
13.已知三棱锥P-ABC的三条侧棱PA、PB、PC两两垂直,D是底面三角形内一点,且∠DPA=450,∠DPB=600,则∠DPC=__________
答案:600
14.正方体AC1中,过点A作截面,使正方体的12条棱所在直线与截面所成的角都相等,试写出满足条件的一个截面____________
15.一个直角三角形的两条直角边长为2和4,沿斜边高线折成直三面角,则两直角边所夹角的余弦值为_____议程。
16.某地球仪上北纬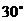 ,纬线的长度为
,纬线的长度为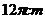 ,该地球仪的半径是_____cm,表面积是_____ cm2。
,该地球仪的半径是_____cm,表面积是_____ cm2。
17.自半径为R的球面上一点P引球的两两垂直的弦PA、PB、PC,则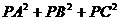 =_____。
=_____。
18.直二面角α-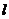 -β的棱
-β的棱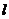 上有一点A,在平面α、β内各有一条射线AB,AC与
上有一点A,在平面α、β内各有一条射线AB,AC与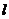 成450,AB
成450,AB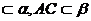 ,则∠BAC=
。
,则∠BAC=
。
19.直线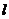 与平面α成角为300,
与平面α成角为300,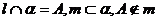 则m与
则m与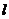 所成角的取值范围是
所成角的取值范围是
20.若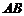 的中点
的中点 到平面
到平面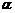 的距离为
的距离为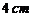 ,点
,点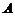 到平面
到平面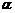 的距离为
的距离为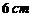 ,则点
,则点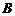 到平面
到平面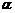 的距离为_________
的距离为_________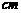 。
。
21.已知直线L∩平面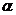 =O,A、B∈L,
=O,A、B∈L,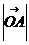 = 4 ,
= 4 ,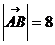 ;点A到平面
;点A到平面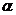 距离为1,则点B到平面
距离为1,则点B到平面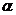 的距离为
。
的距离为
。
22.异面直线a
, b所成的角为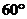 ,过空间一定点P,作直线L,使L与a ,b 所成的角均为
,过空间一定点P,作直线L,使L与a ,b 所成的角均为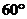 ,这样的直线L有
条。
,这样的直线L有
条。
23四面体的一条棱长为x,其它各棱长为1,若把四面体的体积V表示成x的函数f(x),则f(x)的增区间为 ,减区间为 。
24在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是AB和AD的中点,则点A1到平面为EF的距离为
25.P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和为最大值是
答案:BABAC ,①ADCA,CBBCC,DDBAD,BCDA
1. 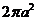 。
2.
。
2. 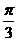 。3.
。3. 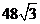 。
4.
。
4. 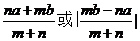 5.
16或64 6.
7个
5.
16或64 6.
7个
7.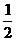 8. 50° 9. 30°
10. (
8. 50° 9. 30°
10. (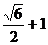 )r 11.
)r 11. 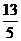 12
12 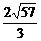 cm 13. 600
cm 13. 600
14. 面AD1C 15.
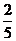 16.
16. 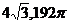 17.
17. 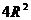 18. 600或1200
18. 600或1200
19. [ 300
, 900] 20. 2、14 21. 1或3 22. 三条
23. (0,
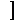
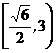
24. 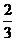 25.
25. 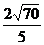
1.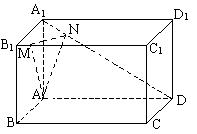 .如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1)
.如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1)  ;
;
(2) 直线AD与平面ANM所成的角的大小;
(3) 平面ANM与平面ABCD所成角(锐角)的大小.
解:(1) 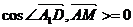
(2) 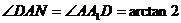
(3) 设平面AMN与平面ABCD所成的角(锐角)为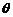 ,则
,则
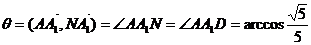
2..点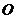 是边长为4的正方形
是边长为4的正方形 的中心,点
的中心,点 ,
,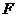 分别是
分别是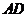 ,
,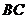 的中点.沿对角线
的中点.沿对角线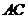 把正方形
把正方形 折成直二面角D-AC-B.
折成直二面角D-AC-B.
(Ⅰ)求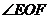 的大小;
的大小; 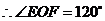
(Ⅱ)求二面角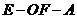 的大小.
的大小.  .
.
.
3..斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成450角,求这个三棱柱的侧面积。 侧(1+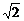 )ab
)ab
4.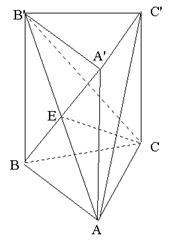 .如图在三棱柱ABC-
.如图在三棱柱ABC- 中,已知底面ABC是底角等于
中,已知底面ABC是底角等于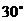 ,底边AC=
,底边AC=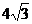 的等腰三角形,且
的等腰三角形,且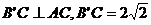 ,面
,面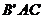 与面ABC成
与面ABC成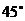 ,
,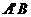 与
与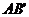 交于点E。
交于点E。
1)
求证: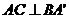 ;
;
2)
求异面直线AC与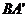 的距离;
的距离;
3)
求三棱锥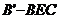 的体积。
的体积。
2) 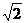 3)
3)
4.如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M点的最短路线长为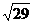 ,设这条最短路线与C1C的交点为N。求
,设这条最短路线与C1C的交点为N。求
4)
该三棱柱的侧面展开图的对角线长;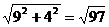
5) PC和NC的长;
6)
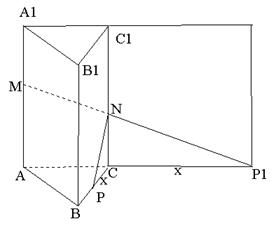 平面NMP和平面ABC所成二面角(锐角)的大小(用反三角函数表示)
平面NMP和平面ABC所成二面角(锐角)的大小(用反三角函数表示)
正解:① 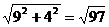
②

③