
1.集合A={1,2,5},B={1,3,5},则A∩B= ▲ .
2.圆柱的底面周长为5cm,高为2cm,则圆柱的侧面积为 ▲ cm2.
3.命题 “对任意 ,都有
,都有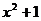 ≥
≥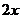 ”的否定是
▲
.
”的否定是
▲
.
4.教师出了一份共3道题的测试卷,每道题1分,全班得3分,2分,1分,0分的学生所占比例分别为30%,40%,20%,10%,若全班30人,则全班同学的平均分是 分.
5.复数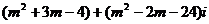 (
(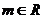 )是纯虚数,则(
)是纯虚数,则(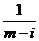 )2的值为
)2的值为
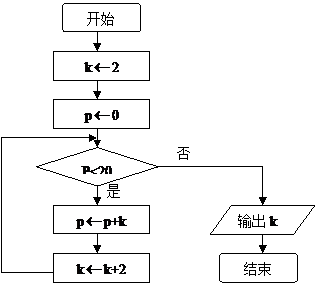
6.若执行下面的程序图的算法,则输出的k的值为 ▲ .
7.不共线的向量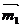 ,
,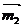 的模都为2,若
的模都为2,若 ,
,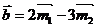 ,则两向量
,则两向量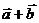 与
与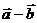 的夹角为
▲
.
的夹角为
▲
.
8.方程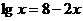 的根
的根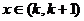 ,
,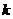 ∈Z,则
∈Z,则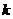 =
▲
.
=
▲
.
9.若三角形ABC的三条边长分别为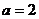 ,
,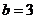 ,
,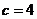 ,
,
则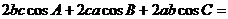 ▲
.
▲
.
10.城市一年中12个月的平均气温与月份的关系可近似地用三角函数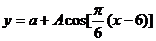 (
( =1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为 ℃.
=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28℃,12月份的月平均气温最低,为18℃,则10月份的平均气温值为 ℃.
11.已知数列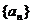 的通项公式为
的通项公式为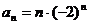 ,则数列{
,则数列{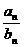 }成等比数列是数列
}成等比数列是数列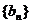 的通项公式为
的通项公式为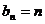 的
条件(对充分性和必要性都要作出判断)
的
条件(对充分性和必要性都要作出判断)
12.已知直线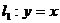 ,
,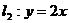 ,
,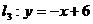 和l4:
和l4: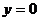 ,由
,由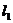 ,
,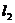 ,
,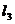 围成的三角形区域记为D,一质点随机地落入由直线l2,l3,l4围成的三角形区域内,则质点落入区域D内的概率为 ▲
.
围成的三角形区域记为D,一质点随机地落入由直线l2,l3,l4围成的三角形区域内,则质点落入区域D内的概率为 ▲
.
13.有一种计算机病毒可以通过电子邮件进行传播,如果第一轮被感染的计算机数是1台,并且以后每一台已经被感染的计算机都感染下一轮未被感染的3台计算机,则至少经过 ▲ 轮后,被感染的计算机总数超过2000台.
14.观察下列恒等式:
∵ 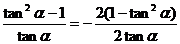 ,∴
,∴
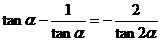 -------①
-------①
∴ 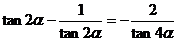 -------②∴
-------②∴
 ------③
------③
由此可知: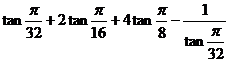 =
.
=
.