
1.()已知直线x+2y-3=0与圆x2+y2+x-6y+m=0相交于P、Q两点,O为坐标原点,若OP⊥OQ,则m等于( )
A.3 B.-3 C.1 D.-1
2.()中心在原点,焦点在坐标为(0,±5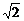 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为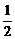 ,则椭圆方程为( )
,则椭圆方程为( )

3.()直线l的方程为y=x+3,在l上任取一点P,若过点P且以双曲线12x2-4y2=3的焦点作椭圆的焦点,那么具有最短长轴的椭圆方程为_________.
4.()已知圆过点P(4,-2)、Q(-1,3)两点,且在y轴上截得的线段长为4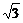 ,则该圆的方程为_________.
,则该圆的方程为_________.
5.()已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=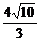 ,试求椭圆的方程.
,试求椭圆的方程.
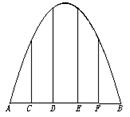
6.()某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长.
7.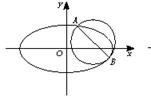 ()已知圆C1的方程为(x-2)2+(y-1)2=
()已知圆C1的方程为(x-2)2+(y-1)2=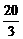 ,椭圆C2的方程为
,椭圆C2的方程为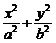 =1(a>b>0),C2的离心率为
=1(a>b>0),C2的离心率为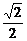 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
难点23 求圆锥曲线方程 求指定的圆锥曲线的方程是高考命题的重点,主要考查学生识图、画图、数形结合、等价转化、分类讨论、逻辑推理、合理运算及创新思维能力,解决好这类问题,除要求同学们熟练掌握好圆锥曲线的定义、性质外,命题人还常常将它与对称问题、弦长问题、最值问题等综合在一起命制难度较大的题,解决这类问题常用定义法和待定系数法. ●难点磁场 1.()双曲线=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________. 参考答案
参考答案
难点磁场
1.解析:设F1(-c,0)、F2(c,0)、P(x,y),则
|PF1|2+|PF2|2=2(|PO|2+|F1O|2)<2(52+c2),
即|PF1|2+|PF2|2<50+2c2,
又∵|PF1|2+|PF2|2=(|PF1|-|PF2|)2+2|PF1|.|PF2|,
依双曲线定义,有|PF1|-|PF2|=4,
依已知条件有|PF1|.|PF2|=|F1F2|2=4c2
∴16+8c2<50+2c2,∴c2<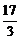 ,
,
又∵c2=4+b2<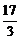 ,∴b2<
,∴b2<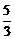 ,∴b2=1.
,∴b2=1.
答案:1
2.解法一:设所求圆的圆心为P(a,b),半径为r,则点P到x轴、y轴的距离分别为|b|、|a|
∵圆P截y轴所得弦长为2,∴r2=a2+1
又由题设知圆P截x轴所得劣弧对的圆心角为90°,故弦长|AB|=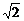 r,故r2=2b2,从而有2b2-a2=1
r,故r2=2b2,从而有2b2-a2=1
又∵点P(a,b)到直线x-2y=0的距离d=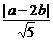 ,
,
因此,5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1,
当且仅当a=b时上式等号成立,此时5d2=1,从而d取最小值,为此有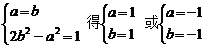 ,
,
∵r2=2b2, ∴r2=2
于是所求圆的方程为:(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2
解法二:设所求圆P的方程为(x-a)2+(y-b)2=r2(r>0)
设A(0,y1),B(0,y2)是圆与y轴的两个交点,则y1、y2是方程a2+(y-b)2=r2的两根,
∴y1,2=b±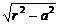
由条件①得|AB|=2,而|AB|=|y1-y2|,得r2-a2=1
设点C(x1,0)、D(x2,0)为圆与x轴的两个交点,则x1,x2是方程(x-a)2+b2=r2的两个根,
∴x1,2=a±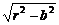
由条件②得|CD|=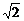 r,又由|CD|=|x2-x1|,得2b2=r2,故2b2=a2+1
r,又由|CD|=|x2-x1|,得2b2=r2,故2b2=a2+1
设圆心P(a,b)到直线x-2y=0的距离为d=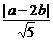
∴a-2b=± d,得a2=(2b±
d,得a2=(2b± d)2=4b2±4
d)2=4b2±4 bd+5d2
bd+5d2
又∵a2=2b2-1,故有2b2±4 bd+5d2+1=0.把上式看作b的二次方程,
bd+5d2+1=0.把上式看作b的二次方程,
∵方程有实根.
∴Δ=8(5d2-1)≥0,得5d2≥1.
∴dmin=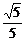 ,将其代入2b2±4
,将其代入2b2±4 bd+5d2+1=0,
bd+5d2+1=0,
得2b2±4b+2=0,解得b=±1.
从而r2=2b2=2,a=±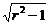 =±1
=±1
于是所求圆的方程为(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2
歼灭难点训练
一、1.解析:将直线方程变为x=3-2y,代入圆的方程x2+y2+x-6y+m=0,
得(3-2y)2+y2+(3-2y)+m=0.
整理得5y2-20y+12+m=0,设P(x1,y1)、Q(x2,y2)
则y1y2=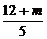 ,y1+y2=4.
,y1+y2=4.
又∵P、Q在直线x=3-2y上,
∴x1x2=(3-2y1)(3-2y2)=4y1y2-6(y1+y2)+9
故y1y2+x1x2=5y1y2-6(y1+y2)+9=m-3=0,故m=3.
答案:A
2.解析:由题意,可设椭圆方程为: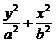 =1,且a2=50+b2,
=1,且a2=50+b2,
即方程为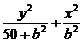 =1.
=1.
将直线3x-y-2=0代入,整理成关于x的二次方程.
由x1+x2=1可求得b2=25,a2=75.
答案:C
二、3.解析:所求椭圆的焦点为F1(-1,0),F2(1,0),2a=|PF1|+|PF2|.
欲使2a最小,只需在直线l上找一点P.使|PF1|+|PF2|最小,利用对称性可解.
答案: =1
=1
4.解析:设所求圆的方程为(x-a)2+(y-b)2=r2
则有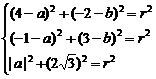
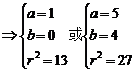
由此可写所求圆的方程.
答案:x2+y2-2x-12=0或x2+y2-10x-8y+4=0
三、5.解:|MF|max=a+c,|MF|min=a-c,则(a+c)(a-c)=a2-c2=b2,
∴b2=4,设椭圆方程为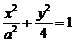 ①
①
设过M1和M2的直线方程为y=-x+m ②
将②代入①得:(4+a2)x2-2a2mx+a2m2-4a2=0 ③
设M1(x1,y1)、M2(x2,y2),M1M2的中点为(x0,y0),
则x0=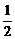 (x1+x2)=
(x1+x2)=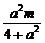 ,y0=-x0+m=
,y0=-x0+m=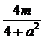 .
.
代入y=x,得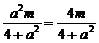 ,
,
由于a2>4,∴m=0,∴由③知x1+x2=0,x1x2=-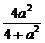 ,
,
又|M1M2|=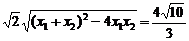 ,
,
代入x1+x2,x1x2可解a2=5,故所求椭圆方程为: =1.
=1.
6.解:以拱顶为原点,水平线为x轴,建立坐标系,
如图,由题意知,|AB|=20,|OM|=4,A、B坐标分别为(-10,-4)、(10,-4)
设抛物线方程为x2=-2py,将A点坐标代入,得100=-2p×(-4),解得p=12.5,
于是抛物线方程为x2=-25y.
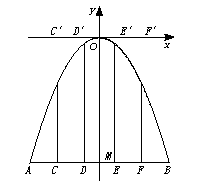
由题意知E点坐标为(2,-4),E′点横坐标也为2,将2代入得y=-0.16,从而|EE′|=
(-0.16)-(-4)=3.84.故最长支柱长应为3.84米.
7.解:由e=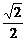 ,可设椭圆方程为
,可设椭圆方程为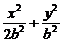 =1,
=1,
又设A(x1,y1)、B(x2,y2),则x1+x2=4,y1+y2=2,
又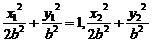 =1,两式相减,得
=1,两式相减,得 =0,
=0,
即(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.
化简得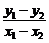 =-1,故直线AB的方程为y=-x+3,
=-1,故直线AB的方程为y=-x+3,
代入椭圆方程得3x2-12x+18-2b2=0.
有Δ=24b2-72>0,又|AB|=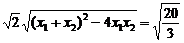 ,
,
得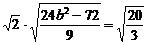 ,解得b2=8.
,解得b2=8.
故所求椭圆方程为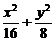 =1.
=1.