
1. 设全集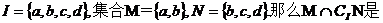
A 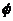 B
B 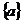 C
C 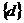 D
D 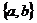
2 不等式
不等式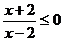 的解集是
的解集是
A 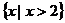 B
B 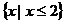 C
C 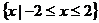 D
D 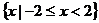
3
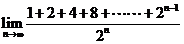 的值等于
的值等于
A 0 B 1 C -1 D 不存在
4 若0<a<1,在区间(-1,0)上函数
若0<a<1,在区间(-1,0)上函数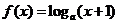 是
是
A增函数且f(x) >0 B增函数且f(x) <0 C减函数且f(x) >0
D减函数且f(x) >0
5. 函数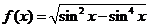 的最小正周期是
的最小正周期是
A 2π B π C 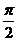 D
D 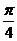
6 若集合A=
若集合A=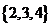 ,B=
,B=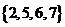 ,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
,从这两个集合中各取一个元素作为平面直角坐标系中点的坐标,能够确定的不同点的个数为
A 11 B 12 C 23 D 24
7 已知x
已知x y满足约束条件
y满足约束条件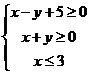 ,则
,则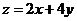 的最小值是
的最小值是
A 5 B -6 C 10 D -10
8 若0<a<1
若0<a<1 0<b<1,且
0<b<1,且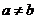 ,则下列各式中值最大的是
,则下列各式中值最大的是
 A
A 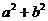 B
B 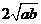 C
C 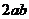 D
D 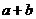
9 已知E
已知E F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF
F分别是正方形ABCD的边AB和CD中的中点,沿EF把正方形拆成一个直二面角(如图),则异面直线BF ED所成角的余弦值为
ED所成角的余弦值为
A 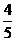 B
B 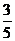 C
C 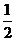 D
D 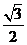
 10
10 某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6
某港口水深度y是时间t的函数(0≤t≤24,单位:小时)的函数,记作y=f(t),其曲线可以近似的看成函数y=Asinωt+b的图象(如图),一般情况下船舶航行是,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只须不碰海底即可),某船的吃水深度(船底离水面的距离)为6 5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
5m,如果该船必须在同一天内(24小时)安全进出港,则它能在港口内停留最长的时间为(进出港所需时间忽略不计)
A 14小时 B 15小时
C 16小时 D 17小时
11 复数
复数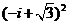 的虚部是
的虚部是 
12 若
若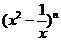 展开式的第6项是x的一次项,那么n=
展开式的第6项是x的一次项,那么n= 
13 曲线C:
曲线C: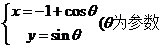 )的普通方程是
,如果曲线C与直线x+m=0有公共点,那么实数m的取值范围是
)的普通方程是
,如果曲线C与直线x+m=0有公共点,那么实数m的取值范围是 
14 如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
如图是某企业近几年来关于生产销售的一张统计图表,则针对该企业近几年的销售情况,有以下几种说法:
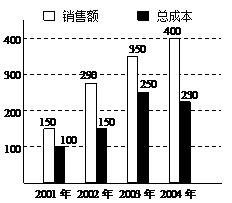 ①这几年该企业的利润逐年提高;(注:利润=销售额-总成本)
①这几年该企业的利润逐年提高;(注:利润=销售额-总成本)
②2001年至2002年是该企业销售额增长最快的一年;
③2002年至2003年是该企业销售额增长最慢的一年;
④2003年至2004年是该企业销售额增长最慢,但是由于总成本有所下降,因而2004年该企业的利润比上一年仍有所增长
其中说法正确的是 (注:把你认为正确的说法的代号都填上)
15 (本小题满分13分)
(本小题满分13分)
在等差数列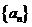 中,
中,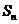 表示数列的前n项和,已知
表示数列的前n项和,已知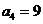 ,
,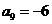 ,求满足
,求满足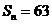 的n值
的n值
16 (本小题满分13分)
(本小题满分13分)
一出租车司机开车从饭店到火车站,途中要过六个交通岗 假设他在各交通岗遇到红灯这一事件是相互独门的,并且概率都是
假设他在各交通岗遇到红灯这一事件是相互独门的,并且概率都是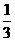

(1) 求这位司机遇到红灯前,连续两个交通岗未遇到红灯的概率;
(2)
求这位司机在途中遇到红灯数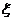 的期望和方差
的期望和方差
17 (本小题满分13分)
(本小题满分13分)
如图,四棱锥P-ABCD的底面ABCD是边长为2的正方形,侧面PAB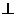 底面ABCD,PA=PB=4,E为PD的中点,过直线BC和点E的平面与棱PA交于点F
底面ABCD,PA=PB=4,E为PD的中点,过直线BC和点E的平面与棱PA交于点F
(1)
 求证:EF
求证:EF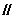 AD
AD
(2)
求直线PC与截面BCEF所成的角
18 (本小题满分13分)
(本小题满分13分)
设函数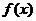 是定义在
是定义在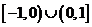 上的奇函数,当
上的奇函数,当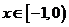 时,
时,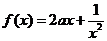
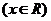

(1)
当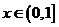 时,求
时,求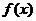 的解析式;
的解析式;
(2)
若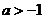 ,试判断
,试判断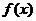 在
在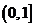 上的单调性,并证明你的结论
上的单调性,并证明你的结论
19 (本小题满分14分)
(本小题满分14分)
今年我市的一个农贸公司计划收购某种农产品,如果按去年各季度该农产品市场价的最佳近似值m收购,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万担 政府为了鼓励收购公司收购这种农产品,决定征收税率降低x个百分点,预测收购量可增加2个百分点
政府为了鼓励收购公司收购这种农产品,决定征收税率降低x个百分点,预测收购量可增加2个百分点
(1) 经计算农贸公司的收购价为m=200(元/担),写出降低征税率后,税收y(万元)与x的函数关系式;;
(2)
要使此项税收值在税率调节后,不少于原计划收购的税收值的83 2%,试确定x的取值范围
2%,试确定x的取值范围
20 (本小题满分14分)
(本小题满分14分)
在平面直角坐标系中,已知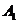 (-3,0)
(-3,0)
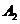 (3,0)
(3,0) P(x,y)
P(x,y) M(
M(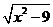 ,0),若实数
,0),若实数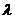 使向量
使向量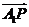

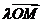

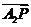 满足
满足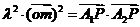
(1) 求P点的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)
当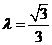 时,过点
时,过点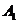 且斜率为1的直线与(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使
且斜率为1的直线与(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使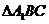 为正三角形
为正三角形
08高考数学模拟试题 本试卷分选择题和非选择题两部分,共4页,满分150分 考试用时120分钟 1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上 用2B铅笔将答题卡上试卷类型(A)涂黑 在答题卡右上角“试室号”栏填写本科目试室号,在“座位号列表”内填写座位号,并用2B铅笔将相应的信息点涂黑 2. 选择题每小题选出后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上 3. 非选择题必须用黑色的铅笔或签字笔参考答案
高中数学综合训练系列试题(23)
参考答案及评分标准
一、选择题 BDBCC CBDAC
二、填空题 11
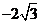 ;12
;12 8;13
8;13
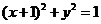 (3分),0≤m≤2(2分);
14
(3分),0≤m≤2(2分);
14 ②④
②④
三、解答题
15 设等差数列的首项为
设等差数列的首项为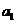
 公差为d,由已知条件可列方程
公差为d,由已知条件可列方程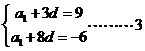 分,
分,
解得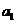 =18,d=-3
=18,d=-3 7分
7分
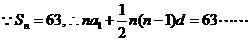 9分
9分
即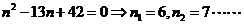 12分
12分
 满足条件的n值分别是6和7
满足条件的n值分别是6和7
 13分
13分
16 解:(1)这位司机在第i,i+1(1
解:(1)这位司机在第i,i+1(1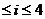 )个交通岗未遇到红灯,在第i+2个交通岗遇到红灯,所以
)个交通岗未遇到红灯,在第i+2个交通岗遇到红灯,所以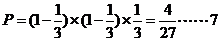 分
分
(2)由题意可知,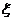 -
-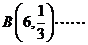 9分
9分 所以
所以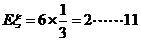 分,
分,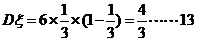 分
分
17 (1)证明:在正方形ABCD中,BC∥AD,且BC
(1)证明:在正方形ABCD中,BC∥AD,且BC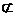 面PAD,所以BC∥D面PAD………2分
面PAD,所以BC∥D面PAD………2分
面PAD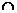 面ABCD=EF,所以BC∥EF………4分 又因为BC∥AD,所以EF∥AD………5分
面ABCD=EF,所以BC∥EF………4分 又因为BC∥AD,所以EF∥AD………5分
(2)解:取AB中点O,CD中点G,C O为原点,AB OG
OG OP所在直线为x轴
OP所在直线为x轴 y轴
y轴 z轴建立空间直角坐标系,则A(-1,0,0),B(1,0,0),C(1,2,0),P(0,0,
z轴建立空间直角坐标系,则A(-1,0,0),B(1,0,0),C(1,2,0),P(0,0, )……7分 由(1)知EF∥AD,E为PD的中点,所以F为PA的中点,
)……7分 由(1)知EF∥AD,E为PD的中点,所以F为PA的中点,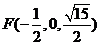 ……8分
……8分
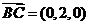 ,
,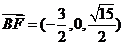 ,
,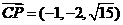 ……9分
……9分
设面BCEF的一个法向量为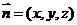 ,由
,由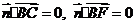 得
得
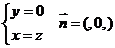 ………10分
cos<
………10分
cos<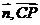 >=
>=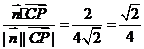 ………12分
………12分
∴直线PC与面BCEF所成的角是arcsin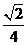 …………13分
…………13分
18 (1)解:任意
(1)解:任意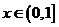 ,则
,则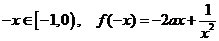 ………3分
………3分
∵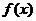 是奇函数,∴
是奇函数,∴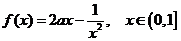 ………7分
………7分
(2)证明: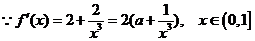 ………10分
………10分
∴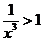 又知a>-1,∴
又知a>-1,∴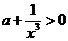 …………12分
…………12分
即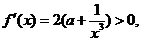 ∴
∴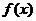 在
在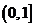 上单调递增………13分
上单调递增………13分
19 解(1)由已知条件可知:降低征税率为(10-x)﹪,农产品收购量为
解(1)由已知条件可知:降低征税率为(10-x)﹪,农产品收购量为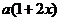 ﹪,农贸公司收购农产品总额为200
﹪,农贸公司收购农产品总额为200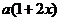 ﹪………6分
﹪………6分
∴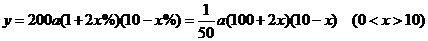 ………8分
………8分
(2)由题意知: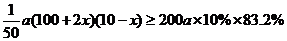 ………10分
………10分
即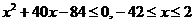 ………12分
………12分
∵0<x<10,∴0<x≤2………14分
答:略
20 解:(1)由已知可得
解:(1)由已知可得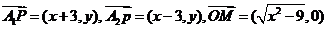 ………1分
………1分
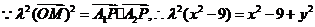
即P点的轨迹方程是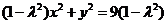 ………3分
………3分
当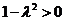 且
且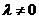 ,即
,即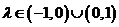 时,有
时,有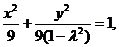 P点的轨迹是椭圆
P点的轨迹是椭圆
当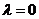 时,方程为
时,方程为 的轨迹是圆
的轨迹是圆
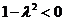 ,即
,即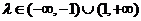 时,方程为
时,方程为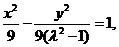 P点的轨迹是双曲线
P点的轨迹是双曲线
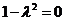 ,即
,即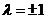 时,方程为y=0, P点的轨迹是直线
时,方程为y=0, P点的轨迹是直线 ………7分
………7分
(2)过点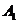 且斜率为1的直线方程为y=x+3………8分
且斜率为1的直线方程为y=x+3………8分
当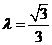 时,曲线方程为
时,曲线方程为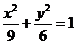
由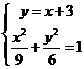 得
得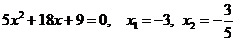 ………10分
………10分
从而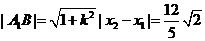 ………12分
………12分
设C(-9,y),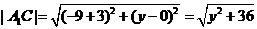
因为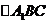 是正三角形,
是正三角形,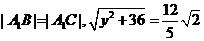 ,即
,即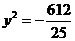 ,无解,
,无解,
所以在直线x=3上找不到点C,使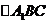 是是正三角形
是是正三角形 ………14分
………14分