1．孔明灯相传是由三国时的诸葛孔明发明的，如图所示．有一盏质量为m的孔明灯升空后沿着东偏北方向匀速上升，则此时孔明灯所受空气的作用力的大小和方向是(　)

A．0　 　　　　　　　　　　　　　　　 B．mg，竖直向上

C．mg，东偏北方向　 　　　　　　　　 D.，东偏北方向

解析：孔明灯做匀速直线运动，故所受合力为0，因此空气的作用力的大小F_空＝mg，方向竖直向上，故选B.

答案：B

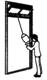
2.人站在自动扶梯的水平踏板上，随扶梯斜向上匀速运动，如图所示．以下说法正确的是(　)

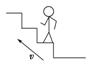
A．人受到重力和支持力的作用

B．人受到重力、支持力和摩擦力的作用

C．人受到的合力不为零

D．人受到的合力方向与速度方向相同

解析：人在竖直方向上受到重力和支持力作用，水平方向上是否受摩擦力作用呢？假设人受到水平向左的静摩擦力作用，与人做匀速运动时所受合力为零不符，故水平方向不应该受力，即人不受摩擦力的作用．

答案：A

3.如图所示，两梯形木块A、B叠放在水平地面上，A、B之间的接触面倾斜．连接A与天花板之间的细绳沿竖直方向．关于两木块的受力，下列说法正确的是(　)

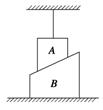
A．A、B之间一定存在摩擦力作用

B．木块A可能受三个力作用

C．木块B可能受到地面的摩擦力作用

D．B受到的地面的支持力一定大于木块B的重力

解析：当绳对A的拉力等于A的重力时，A、B之间没有弹力，也一定没有摩擦力，此时地面对B的支持力等于B的重力，因此选项A、D错误．当绳对A的拉力为零时，由力的平衡知，A应受重力、弹力和B对A的摩擦力共三个力的作用，选项B正确．由整体法可知，地面对B的摩擦力一定为零，选项C错误．

答案：B

4.(2016.淮安模拟)如图所示，两段等长细线串接着两个质量相等的小球a、b，悬挂于O点．现在两个小球上分别加上水平方向的外力，其中作用在b球上的力大小为F，作用在a球上的力大小为2F，则此装置平衡时的位置可能是下图中的(　)

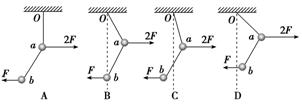
解析：设Oa段绳子与竖直方向的夹角为α，ab段绳子与竖直方向夹角为β.以整个系统为研究对象，受到重力2mg、水平向右的拉力F和Oa绳的拉力作用，根据物体的平衡条件可得tan α＝，且α≠0.以小球b为研究对象，受到重力mg、水平向左的拉力F和ab绳的拉力作用，得tan β＝，由此可见α＜β，C正确．

答案：C

5.(2014.高考上海卷)如图，光滑的四分之一圆弧轨道AB固定在竖直平面内，A端与水平面相切．穿在轨道上的小球在拉力F作用下，缓慢地由A向B运动，F始终沿轨道的切线方向，轨道对球的弹力为F_N.在运动过程中(　)

A．F增大，F_N减小　 　　　　　　　　　 B．F减小，F_N减小

C．F增大，F_N增大　 　　　　　　　　　 D．F减小，F_N增大

解析：小球一直受到重力、支持力、拉力作用，根据共点力平衡，有F＝mgsin α，F_N＝mgcos α(α是弹力与竖直方向的夹角)，随着夹角的增大，支持力逐渐减小，拉力逐渐增大，A项正确．

答案：A

6.如图所示，用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂，小球处于静止状态，弹簧A与竖直方向的夹角为30°，弹簧C水平，则弹簧A、C的伸长量之比为(　)

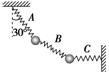
A.∶4　 　　　　　　　　　　　　　 B．4∶

C．1∶2　 　　　　　　　　　　　　　 D．2∶1

解析：弹簧A、C的弹力可看成两小球构成系统的外力，可用整体法分析．以两个小球及弹簧B整体为研究对象，受力分析如图所示，则根据平衡条件，在水平方向有F_Asin 30°＝F_C，即A、C两弹簧的弹力之比F_A∶F_C＝2∶1.由于两弹簧完全相同，根据胡克定律知，两弹簧的伸长量之比x_A∶x_C＝F_A∶F_C＝2∶1，D正确．

答案：D

7.如图所示，两块相互垂直的光滑挡板OP、OQ，OP竖直放置，小球a、b固定在轻弹簧的两端．水平力F作用于b时，a、b紧靠挡板处于静止状态．现保证b球不动，使挡板OP向右缓慢平移一小段距离，则(　)

A．弹簧变长　 　　　　　　　　　　　 B．弹簧变短

C．力F变大　 　　　　　　　　　　　 D．b对地面的压力变大

解析：选a球为研究对象，受力分析如图所示，由画出的平行四边形可知，挡板的弹力F_N变小，弹力F_T逐渐减小，即弹簧的压缩量变短，弹簧变长，选项A正确，B错误；选a球、b球整体为研究对象，由平衡条件可知，F变小，b对地面的压力不变，选项C、D均错．

答案：A

8．如图所示，A、B、C、D是四个完全相同的木块，在图甲中，水平力F作用于B上，A、B处于静止状态，图乙中，竖直弹簧作用于D上，C、D处于静止状态，则关于A、B、C、D的受力情况，下列说法正确的是(　)

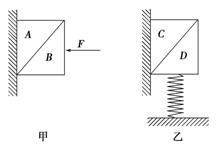
A．图甲中A受五个力，图乙中C受三个力

B．图乙中墙对C可能有摩擦力

C．图甲中墙对A一定没有摩擦力

D．图乙中D对C一定有向右上方的摩擦力

解析：选整体为研究对象，可知图甲中，墙对A一定有向上的摩擦力，而图乙中，墙对C没有摩擦力和支持力，B、C错误．在图乙中，C处于静止状态，其除受重力、D对它的支持力外，一定受到D对其向右上方的摩擦力，D正确．在题图甲中，A受重力、墙的支持力、B的支持力、墙的摩擦力(向上)、B的摩擦力(左下方)，共五个力，A正确．

答案：AD

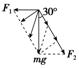
9.如图所示，重为mg的水桶用细绳悬挂在门楣上，一人将水桶拉起使细绳与竖直方向的夹角为30°且细绳绷紧，则人对水桶施加的作用力可能为(　)

A.mg　 　　　　　　　　　　　　　　 B.mg

C.mg　 　　　　　　　　　　　　　　 D.mg

解析：将重力按如图所示的方式分解，F₂与绳的拉力等大反向，F₁与人所施加的力等大反向，由图可知人对水桶施加的作用力的最小值为，故A正确，B、C错误；当人对水桶施加的作用力为水平方向时，施加的作用力大小为mg，D正确．

答案：AD

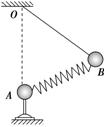
10.(2016.北京海淀区模拟)如图所示，质量均为m的小球A、B用劲度系数为k₁的轻弹簧相连，B球用长为L的细绳悬于O点，A球固定在O点正下方L处，当小球B平衡时，绳子所受的拉力为F_T1，弹簧的弹力为F₁；现把A、B间的弹簧换成原长相同但劲度系数为k₂(k₂＞k₁)的另一轻弹簧，在其他条件不变的情况下仍使系统平衡，此时绳子所受的拉力为F_T2，弹簧的弹力为F₂.下列关于F_T1与F_T2、F₁与F₂大小之间的关系，正确的是(　)

A．F_T1＞F_T2　 　　　　　　　　　　　　 B．F_T1＝F_T2

C．F₁＜F₂　 　　　　　　　　　　　　　 D．F₁＝F₂

解析：以小球B为研究对象，进行受力分析，由平衡条件可知，弹簧的弹力F和绳子的拉力F_T的合力F_合与重力mg大小相等，方向相反，即F_合＝mg，如图所示，由三角形相似得(力的三角形和几何三角形相似)：＝＝，又OA＝OB＝L，得F_T＝mg，F＝mg，故绳子的拉力F_T只与小球B的重力有关，与弹簧的劲度系数无关，所以F_T1＝F_T2.当弹簧的劲度系数变大时，弹簧的压缩量减小，故长度x增加，F₂＞F₁，A、D错误，B、C正确．

答案：BC

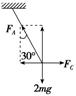
11.(2016.绵阳模拟)如图所示，一球A夹在竖直墙与三角劈B的斜面之间，三角劈的重力为G，劈的底部与水平地面间的动摩擦因数为μ，劈的斜面与竖直墙面是光滑的，设劈的最大静摩擦力等于滑动摩擦力．问：欲使三角劈静止不动，球的重力不能超过多少？

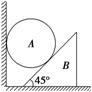
解析：由三角形劈与地面之间的最大静摩擦力可以求出三角形劈所能承受的最大压力，由此可求出球的最大重力．球A与三角形劈B的受力情况分别如图甲、乙所示．

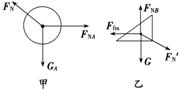
球A在竖直方向的平衡方程为G_A＝F_Nsin 45°

三角形劈的平衡方程为F_fm＝F_N′sin 45°

F_NB＝G+F_N′cos 45°

另有F_fm＝μF_NB

解得F_N′＝

又F_N＝F_N′

联立以上各式可得G_A＝G.

答案：G

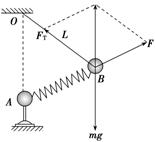
12．如图所示，质量为m₁的物体甲通过三段轻绳悬挂，三段轻绳的结点为O，轻绳OB水平且B端与站在水平面上的质量为m₂的人相连，轻绳OA与竖直方向的夹角θ＝37°，物体甲及人均处于静止

状态．(已知sin 37°＝0.6，cos 37°＝0.8，g取10 m/s².设最大静摩擦力等于滑动摩擦力)

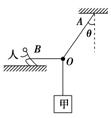
(1)轻绳OA、OB受到的拉力分别是多大？

(2)人受到的摩擦力是多大？方向如何？

(3)若人的质量m₂＝60 kg，人与水平面之间的动摩擦因数μ＝0.3，欲使人在水平面上不滑动，则物体甲的质量m₁最大不能超过多少？

解析：(1)以结点O为研究对象进行受力分析，如图(a)所示，由平衡条件有F_OB－F_OAsin θ＝0，F_OAcos θ－m₁g＝0，联立以上两式解得F_OA＝＝m₁g，F_OB＝m₁gtan θ＝m₁g，故轻绳OA、OB受到的拉力分别为m₁g、m₁g.

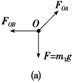
(2)人在水平方向受到OB绳的拉力F_OB′和水平面的静摩擦力作用，F_OB′＝F_OB，受力如图(b)所示，由平衡条件得F_f＝F_OB′＝F_OB＝m₁g，方向水平向左．

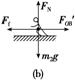
(3)当人刚要滑动时，甲的质量达到最大，此时人受到的静摩擦力达到最大值，有F_fm＝μm₂g

由平衡条件得F_OBm′＝F_fm，

又F_OBm′＝m_1mgtan θ＝m_1mg，

联立得m_1m＝＝＝24 kg.

即物体甲的质量m₁最大不能超过24 kg.

答案：(1)m₁g　m₁g

(2)m₁g　方向水平向左　(3)24 kg