1－7题只有一项符合题目要求，8－10题有多项符合题目要求．

1．(2015.天津)中国古人对许多自然现象有深刻认识，唐人张志和在《玄真子.涛之灵》中写道：“雨色映日而为虹”．从物理学的角度看，虹是太阳光经过雨滴的两次折射和一次反射形成的．下图是彩虹成因的简化示意图，其中a、b是两种不同频率的单色光，则两光(　)

A．在同种玻璃中传播，a的传播速度一定大于b光

B．以相同角度斜射到同一玻璃板透过平行表面后，b光侧移量大

C．分别照射同一光电管，若b光能引起光电效应．a光也一定能

D．以相同的入射角从水中射入空气．在空气中只能看到一种光时，一定是a光

答案　C

2．(2013.浙江)与通常观察到的月全食不同，小虎同学在2012年12月10日晚观看月全食时，看到整个月亮是暗红的．小虎画了月全食的示意图，并提出了如下猜想，其中最为合理的是(　)

A．地球上有人用红色激光照射月球

B．太阳照射到地球的红光反射到月球

C．太阳光中的红光经地球大气层折射到月球

D．太阳光中的红光在月球表面形成干涉条纹

解析　照亮月球所需的光源的能量巨大，人为产生的红色激光不足以照亮月球，A选项不合理；月全食是月食的一种，当月亮、地球、太阳完全在一条直线上的时候，整个月亮全部走进地球的影子里，月亮表面昏暗，形成月全食，地球挡住了太阳射向月球的光，不是反射的光，但是还会有部分光线通过地球大气层发生折射，所以会有部分地球大气层折射后的红色光射向月亮，这就让我们看到了“红月亮”，B选项错误，C选项正确；月球整体为暗红色，不是干涉条纹，D选项错误．

答案　C

3．(2016.浙江宁波)在学习光的色散的时候老师在课堂上做了一个演示实验，让某特制的一束复色光由空气射向一块平行平面玻璃砖(玻璃较厚)，经折射分成两束单色光a、b，已知a光是红光，而b光是蓝光，你认为下图中哪个光路图是正确的(　)

解析　玻璃对蓝光的折射率大于红光的折射率，光线射到玻璃砖上表面时，两束光的入射角θ₁相等，根据折射定律＝n，得到红光的折射角大于蓝光的折射角，则a光在b光的右侧．光线经过玻璃砖上下两个表面两次折射后，出射光线与入射光线平行．

答案　B

设置目的　考查玻璃砖对光路的控制作用、光的折射

4．(2016.福建泉州)为了减少光学元件的反射损失，可在光学元件表面镀上一层增透膜，利用薄膜的干涉相消来减少反射光．如果照相机镜头所镀膜对绿光的折射率为n，厚度为d，它使绿光在垂直入射时反射光完全抵消，那么绿光在真空中的波长λ₀为(　)

A.　　　　　　　　　　　　　 B.

C．4d　 　　　　　　　　　　　　　　　　 D．4nd

解析　本题考查薄膜干涉．设绿光在膜中的波长为λ，则由d＝λ，得λ＝4d，则绿光在真空中的波长为λ₀＝nλ＝4nd.

答案　D

设置目的　考查薄膜干涉

5.(2016.湖南衡阳)有一摆长为l的单摆，悬点正下方某处有一小钉，当摆球经过平衡位置向左摆动时，摆线的上部将被挡住，使摆长发生变化．现使摆球做小角度摆动，图示为摆球从右边最高点M摆至左边最高点N的闪光照片(悬点和小钉未摄入)，P为摆动中的最低点，每相邻两次闪光的时间间隔相等．则小钉距悬点的距离为(　)

A.　 　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　 D．条件不足，无法判断

解析　图中M到P为四个时间间隔，P到N为两个时间间隔，即左半部分单摆的周期是右半部分单摆周期的，根据周期公式T＝2π，可得左半部分单摆的摆长为，即小钉距悬点的距离为，C选项正确．

答案　C

设置目的　考查单摆的振动周期公式、通过图片判断运动情况的能力

6．在杨氏干涉实验中，单缝位于双缝的中央对称轴上，从两个狭缝到达像屏上的某点的光走过的路程相等，该点即为中央亮条纹的位置(即n＝0对应的那条亮条纹)，双缝屏上有上下两狭缝，设想在双缝屏后用一块极薄的玻璃片遮盖下方的缝，则屏上中央亮条纹的位置将(　)

A．向上移动　　　　　　　　　　　　　　 B．向下移动

C．不动　　　　　　　　　　　　　　　　 D．可能向上移动，也可能向下移动

解析　双缝到屏上中央亮条纹O点的距离相等，当下方的狭缝后用一块极薄的玻璃片遮盖住后，由于波在玻璃中传播的波长变小，因此下缝到O点的距离内的波长个数变多，所以屏上对应的到双缝波长个数相等的点下移，即屏上中央亮条纹的位置将向下移动，故本题选B项．(注：在不加特别说明的情况下，单缝S位于双缝S₁、S₂的中央对称轴位置处．)

答案　B

7．实验表明，可见光通过三棱镜时各色光的折射率n随波长λ的变化符合科西经验公式：n＝A++，其中A、B、C是正的常量．太阳光进入三棱镜后发生色散的情形如图所示．则

(　)

A．屏上c处是紫光　 　　　　　　　　　　 B．屏上d处是红光

C．屏上b处是紫光　 　　　　　　　　　　 D．屏上a处是红光

解析　白色光经过三棱镜后产生色散现象，在光屏由上至下(a、b、c、d)依次为红、橙、黄、绿、蓝、靛、紫．由于紫光的折射率最大，所以偏折最大；红光的折射率最小，则偏折程度最小．故屏上a处为红光，屏上d处是紫光，D项正确．

答案　D

8．(2015.德州二模)图a为一列简谐横波在t＝0时刻的波形图，图b为介质中平衡位置在x＝4 m处的质点P的振动图像．下列说法中正确的是(　)

A．质点P的振动频率为4 Hz　　　　　　　 B．横波传播的速度为1 m/s

C．横波沿x轴负方向传播　　　　　　　　 D．在任意4 s内质点P运动的路程为24 cm

解析　根据a、b两图可以读出该波的波长和周期，从而求出波速和频率．t＝0 s时P点在平衡位置上，由b图知下一时刻向下振动，从而确定了该波向右传播．根据质点简谐运动的周期性求出t＝4 s内质点P通过的路程，并能确定t＝1 s时其坐标．A、B项，由a图得到该波的波长为4 m，由b图得到该波的周期为4 s，故波速为v＝＝＝1 m/s，频率为f＝＝ Hz，故A项错误，B项正确；C项，t＝0 s时P点在平衡位置上，由b图知下一时刻P点向下振动，从而确定了该波沿x轴正方向传播，故C项错误；D项，由于4 s即为一个周期，根据质点简谐运动时每个周期内的路程为振幅的4倍，故P点的路程为s＝4A＝4×6 cm＝24 cm，故D项正确．

答案　BD

命题立意　本题旨在考查波长、频率和波速的关系；横波的图像

9．(2015.江山市模拟)两列简谐横波在同种介质中传播，振幅都是5 cm.实线波的频率为2 Hz，沿x轴负方向传播；虚线波沿x轴正方向传播．某时刻两列波在如图所示区域相遇，则(　)

A．虚线波的振动周期为0.75 s

B．在相遇区域会发生干涉现象

C．平衡位置为x＝6 m处的质点此刻速度为零

D．从图示时刻起再经过0.25 s，平衡位置为x＝7 m处的质点的位移y＞0

解析　A项，实线波的频率为2 Hz，周期T₁＝0.5 s，根据图像可知，实线波长λ₁＝4 m，虚线波长λ₂＝6 m，则波速为v＝＝ m/s＝8 m/s.

两列波的传播速度大小相同，所以虚线的振动周期为T₂＝＝ s＝0.75 s，故A项正确；B项，由于两列波的频率不同．所以不能发生干涉现象．故B项错误；C项，平衡位置为x＝6 m处的质点此刻位移为零，两列波单独引起的速度均向下，故合速度向下，不为零，故C项错误；D项，传播速度大小相同．实线波的频率为2 Hz，其周期为0.5 s，由图可知：虚线波的周期为0.75 s，从图示时刻起再经过0.25 s，实线波在平衡位置为x＝7 m处于波峰，而虚线波也处于y轴下方，但不在波谷处，所以质点的合位移y>0，故D项正确．

答案　AD

命题立意　本题旨在考查横波的图像、波长、频率和波速的关系

10．(2015.吉林三模)如图所示，实线是沿x轴传播的一列简谐横波在t＝0时刻的波形图，虚线是这列波在t＝0.2 s时刻的波形图．则(　)

A．这列波的周期可能是1.2 s　　　　　　 B．这列波的波长为12 m

C．这列波可能向左传播4 m　　　　　　　 D．这列波的波速可能是40 m/s

解析　由图可知，该波的波长为12 m，故B项正确；若波向左传播，则s＝(n+)λ＝12n+4(n＝0，1，2，3，…)，s取4时，n＝0，故波可能向左传4 m，故C项正确；设波的周期为T，若波沿x轴正方向传播，则t＝(n+)T₁，得T₁＝＝(n＝0，1，2，3，…)

波速可以为v＝＝20(3n+2)(n＝0，1，2，3，…)

若波沿x轴负方向传播，则t＝(n+)T₂

得T₂＝(n＝0，1，2，3，…)

波速为v＝20(3n+1)(n＝0，1，2，3，…)

由以上公式可知，周期不可能为1.2 s；而波速可为40 m/s，故A项错误，D项正确．

答案　BCD

命题立意　本题旨在考查波长、频率和波速的关系、横波的图像

11．(12分)(2016.北京海淀区)利用插针法可以测量半圆柱形玻璃砖的折射率．实验方法如下：在白纸上作一直线MN，并作出它的一条垂线AB，将半圆柱形玻璃砖(底面的圆心为O)放在白纸上，它的直边与直线MN对齐，在垂线AB上插两个大头针P₁和P₂，然后在半圆柱形玻璃砖的右侧插上适量的大头针，可以确定光线P₁P₂通过半圆柱形玻璃砖后的光路，从而求出玻璃的折射率．实验室中提供的器材除了半圆柱形玻璃砖、木板和大头针外，还有量角器等．

(1)某学生用上述方法测量玻璃的折射率，在他画出的垂线AB上竖直插上了P₁、P₂两枚大头针，但在半圆柱形玻璃砖右侧的区域内，不管眼睛放在何处，都无法透过半圆柱形玻璃砖同时看到P₁、P₂的像，原因________________________，他应该采取的措施是________________________．

(2)为了确定光线P₁P₂通过半圆柱形玻璃砖后的光路，在玻璃砖的右侧，最少应插________枚大头针．

(3)请在半圆柱形玻璃砖的右侧估计所插大头针的可能位置，并用“×”表示，作出光路图．为了计算折射率，应该测量的量(在光路图上标出)，有：____________________，计算折射率的公式是n＝________．

解析　在半圆柱形玻璃砖右侧的区域内，不管眼睛放在何处，都无法透过半圆柱形玻璃砖同时看到P₁、P₂的像，原因是光线P₁P₂垂直于界面进入半圆柱形玻璃砖后，到达圆弧面上的入射角大于临界角，发生全反射现象，光不能从圆弧面折射出来，可以采取减小光线在圆弧面上的入射角，即向上移动半圆柱玻璃砖；因为光线在圆弧面上的出射点已知，只要在玻璃砖的右侧插入1枚大头针，即可确定出射光线；光路图如答案图所示，为了测量折射率的大小，需测量入射角i和折射角r，则折射率n＝.

答案　(1)是光线P₁P₂垂直于界面进入半圆柱形玻璃砖后，到达圆弧面上的入射角大于临界角，发生全反射现象，光不能从圆弧面折射出来。　向上移动半圆柱形玻璃砖，使到达圆弧面上光线的入射角小于临界角。

(2)1

(3)光路图如右图，光在圆弧面上D点发生折射，法线为OD直线，测出入射角i和折射角r，折射率n＝.

设置目的　考查测量介质折射率的实验设计、综合分析问题能力

12．(8分)(2016.湖南岳阳)利用如图所示，

(1)图1中装置研究双缝干涉现象时，有下面几种说法，其中说法正确的是________．

A．将屏移近双缝，干涉条纹间距变窄

B．将滤光片由蓝色的换成红色的，干涉条纹间距变宽

C．将单缝向双缝移动一小段距离后，干涉条纹间距变宽

D．换一个两缝之间距离较大的双缝，干涉条纹间距变窄

E．去掉滤光片后，干涉现象消失

(2)实验中使用的双缝间距为0.025 cm，双缝与屏的距离为50.00 cm.当屏上出现了干涉图样后，通过测微目镜观察第一条亮纹的位置如图2左侧所示x₁＝________ mm，第五条亮纹位置如图2右侧所示．实验中该光波长为________ m(两位有效数字)．

解析　(1)将屏移近双缝，L变小，根据干涉条纹间距公式Δx＝λ，知条纹间距变窄，故A项正确；将滤光片由蓝色的换成红色的，波长变长，根据干涉条纹间距公式Δx＝λ，知条纹间距变宽，B项正确；将单缝向双缝移动一小段距离后，干涉条纹间距不变．故C项错误；换一个两缝之间距离较大的双缝，d增大，根据干涉条纹间距公式Δx＝λ，干涉条纹间距变窄，D项正确；去掉滤光片，则有不同波长的色光发生干涉形成彩色条纹，故E项错误．

(2)图2中左侧螺旋测微器的读数为1 mm+0.01×13.0 mm＝1.130 mm，图2中右侧螺旋测微器的读数为5.5 mm+0.01×38.0 mm＝5.880 mm.根据双缝干涉条纹的间距公式Δx＝λ，得

λ＝＝ m＝5.9×10^{－7 m.}

答案　(1)ABD　(2)1.130　5.9×10^－7

设置目的　考查双缝干涉实验中波长的求解、实验现象的分析

13．(8分)将一劲度系数为k的轻质弹簧竖直悬挂，下端系上质量为m的物块，将物块向下拉离平衡位置后松开，物块上下做简谐运动，其振动周期恰好等于以物块平衡时弹簧的伸长量为摆长的单摆周期．请由单摆周期公式推算出物块做简谐运动的周期T.

解析　单摆周期公式T＝2π，物块平衡位置受力分析可知kl＝mg，解得T＝2π.

答案　T＝2π

设置目的　考查新情境下的迁移能力

14．(10分)(2015.德州二模)如图所示，截面为三角形透明介质的三棱镜，三个顶角分别为∠A＝60°，∠B＝75°，∠C＝45°，介质的折射率n＝，现有一束光线沿MN方向射到棱镜的AB面上，入射角的大小i＝60°，光在真空中的传播速度c＝3×10⁸ m/s，求：

(1)光在棱镜中传播的速率；

(2)画出此束光线进入棱镜后又射出棱镜的光路图，要求写出必要的计算过程．(不考虑返回到AB和BC面上的光线)

解析　(1)光在棱镜中传播的速率应根据公式v＝求解．光在棱镜中传播的速率

v＝＝ m/s＝×10⁸ m/s.

(2)已知折射率n和入射角的正弦sini，根据折射定律n＝求出折射角．由公式sinC＝求得临界角C.由几何知识求出光线射到BC面的入射角，根据入射角与临界角的大小关系，判断光线在BC面上能否发生全反射，再进一步确定此束光线射出棱镜后的方向．设此束光从AB面射入棱镜后的折射角为r，由折射定律n＝，得＝，解得r＝30°.显然光线从AB射入棱镜后的折射光线NP平行于底边AC，由图中几何关系可得，光线在BC面上的入射角θ＝45°

设临界角为C，则由sinC＝＝，sinθ＝

可得θ＞C

故光线在BC面上发生全反射后，根据几何知识和反射定律得知，光线将垂直于底面AC方向由图中Q点射出棱镜．光路如图所示．

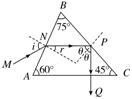
答案　(1)v＝×10⁸ m/s　(2)见解析图

命题立意　本题旨在考查光的折射

15．(10分)(2016.甘肃兰州)一列横波在x轴线上传播着．图中实线表示t₁＝0的波形曲线，虚线表示t₂＝0.005 s时的波形曲线．

(1)设周期大于(t₂－t₁)，如果波向右传播，波速多大？

(2)设周期小于(t₂－t₁)，并且波速为6 000 m/s，求波的传播方向．

解析　(1)如果周期大于(t₂－t₁)，波在0.005 s内传播的距离小于一个波长．如果波向右传播，则传播距离从图中看出为2 m，由此可得波速v_右＝ m/s＝400 m/s；

(2)由图可知λ＝8 m，波的传播距离为s＝vt＝6 000×0.005 m＝30 m＝3λ.说明波向左传播．

答案　(1)400 m/s　(2)向左传播

设置目的　考查波动的传播与周期、波长间的关系、及波动方向的判定方法

16.(12分)(2015.陕西三模)图示的直角三角形ABC是玻璃砖的横截面，∠B＝90°，∠A＝30°，BC边长等于L.一束平行于AB边的光束从AC边上的某点射入玻璃砖，进入玻璃砖后，在BC边上的E点被反射，E点是BC边的中点，EF是从该处反射的光线，且EF恰与AC边平行．求：

(1)玻璃砖的折射率；

(2)该光束从E点反射后，直到第一次有光线从玻璃砖射出所需的时间(真空中的光速用符号“c”表示)．

解析　(1)作出光路图，根据几何知识和全反射规律得到光线在AC面的入射角和折射角，即可求得折射率，

(2)根据全反射临界角公式sinC＝求出临界角C，判断出光线在F点发生全反射，在O₂点不能发生全反射，即该光束经一次反射后，到第一次射出玻璃砖发生在O₂点，根据几何知识求出光线在玻璃砖内传播的距离s，由v＝求出光线在玻璃砖内传播的速度v，即可求得所求的时间

依题意，光在玻璃砖中的传播路径如右图所示．

可见，光在O₁点的入射角为60°，折射角为30°.

①玻璃的折射率n＝＝

②因为>sinC＝>，所以这种玻璃的临界角C大于30°，小于60°.

故从E点反射出的光线，将在F点发生全反射，在O₂点才有光线第一次射出玻璃砖．由几何知识可知：EF＝L，FO₂＝L；

光在这种玻璃中的传播速度v＝＝.

故光从E点传播到O₂点用时t＝＝.

答案　(1)玻璃砖的折射率为

(2)该光束从E点反射后，直到第一次有光线从玻璃砖射出所需的时间为

命题立意　本题旨在考查光的折射