1. 在△ABC中,∠A=90°,CD平分∠ACB,DE⊥BC于点E,若AB=6,则DE+DB=( )
A.4  B. 5 C. 6 D. 7
B. 5 C. 6 D. 7

2.如图,从下列四个条件:①BC=B′C, ②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如图2,在△ABC中,AB=AC,∠BAD=30 ,AD=AE,则∠EDC=(
)
,AD=AE,则∠EDC=(
)
 A.10
A.10 B. 12.5
B. 12.5 C.15
C.15 D.20
D.20

4.如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB于E,DF⊥AC于F,则图中全等三角形共有( )
2对 B、3对 C、4对 D、5对
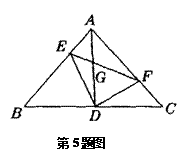
5.如图,在等腰直角△ABC中,AD为斜边上的高,以D为端点任作两条互相垂直的射线与两腰相交于E、F,连结EF与AD相交于G,则∠AED与∠AGF的关系为( )
A.∠AED>∠AGF B.∠AED=∠AGF C.∠AED<∠AGF D.不能确定
6.等腰三角形ABC的底边BC=8cm,且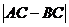 =2cm,则腰AC的长为( )
=2cm,则腰AC的长为( )
A.10cm或6cm B.10cm C.6cm D.8cm或6cm
7.已知等腰三角形的两边a,b,满足 +(2a+3b-13)2=0,则此等腰三角形的周长为( ) A.7或8 B.6或10 C.6或7 D.7或10
+(2a+3b-13)2=0,则此等腰三角形的周长为( ) A.7或8 B.6或10 C.6或7 D.7或10
8.直角三角形的周长为12cm,斜边长为5cm,则其面积为( )
A、12cm2 B、10cm2 C、8cm2 D、6cm2
9. 如图所示,已知△ABC是不等边三角形,P是△ABC所在平而上一点,P不与点A重合,要想使△PBC与△A
如图所示,已知△ABC是不等边三角形,P是△ABC所在平而上一点,P不与点A重合,要想使△PBC与△A BC全等,则这样的P点有(
)
BC全等,则这样的P点有(
)
A.1个 B.2个
C.3个 D.4个
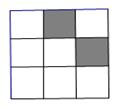
10.如图,正方形网格中,已有两 个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
( )
个小正方形被涂黑,再将图其余小正方形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的方法有
( )

 A.5
B.6 C.4
D.7
A.5
B.6 C.4
D.7
第10题 第11题
11.如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是
( )
A. 6 cm B. 8 cm
C. 10 cm D. 12 cm
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是
( )
A. 6 cm B. 8 cm
C. 10 cm D. 12 cm
12. 如果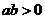 ,
, ,则直线
,则直线 不通过( )
不通过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
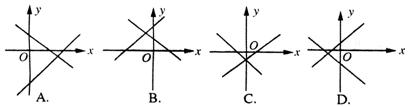
13.如下图,两直线 和
和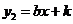 在同一坐标系内图象的位置可能是( )
在同一坐标系内图象的位置可能是( )
14.函数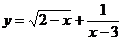 中,自变量x的取值范围是(
)
中,自变量x的取值范围是(
)
A.x≤2 B.x=3 C.x<2且x ≠3 D.x ≤2且x≠3
15.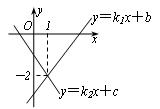 直线
直线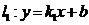 与直线
与直线 在同一平面直角坐标系中的图象如图所示,则关于
在同一平面直角坐标系中的图象如图所示,则关于 的不等式
的不等式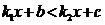 的解集为( ).
的解集为( ).
A. x>1 B. x<1 C. x>-2 D. x<-2
16.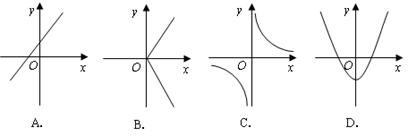 下列曲线中,表示
下列曲线中,表示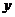 不是
不是 的函数是( )
的函数是( )
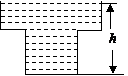
17. 某蓄水池的横断面示意图如下图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度
某蓄水池的横断面示意图如下图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度 和放水时间
和放水时间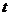 之间的关系的是( )
之间的关系的是( )
18.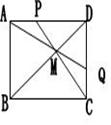 如图,正方形ABCD的对角线BD上一点M,BM=BC,CM的延长线交AD于P,AM延长线交CD于Q,则∠CMQ= ( ).
如图,正方形ABCD的对角线BD上一点M,BM=BC,CM的延长线交AD于P,AM延长线交CD于Q,则∠CMQ= ( ).
A.25° B.45°
C.67.5° D.30.5°
19.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=( )
A.2
B.3
C. 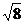 D.
D.
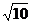
20.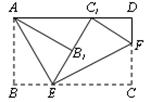 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=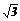 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ).
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ).
A、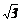 B、2
C、3
D、
B、2
C、3
D、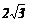
21.如图1,在矩形MNPQ中,动点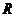 从点
从点 出发,沿N→P→Q→M方向运动至点
出发,沿N→P→Q→M方向运动至点 处停止.设点
处停止.设点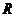 运动的路程为
运动的路程为 ,△MNR的面积为
,△MNR的面积为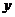 ,如果y关于
,如果y关于 的函数图象如图2所示,则当x=9时,点R应运动到(
) 、
的函数图象如图2所示,则当x=9时,点R应运动到(
) 、
A. 处 B.
处 B. 处
C.Q处 D.
处
C.Q处 D.

22.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是__________.
23. 如右图,已知在△ABC中,
如右图,已知在△ABC中,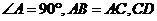 平
平
分 ,
, 于
于 ,若
,若 ,则
,则
 的周长为
的周长为  .
.
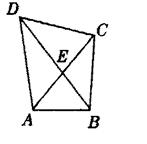
24.如右图,四边形ABCD中,对角线AC与BD相交于E点,若AC平分
∠DAB,且AB=AE,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;
③∠DBC= ∠DAB;④△ABE是等边三角形.
∠DAB;④△ABE是等边三角形.
请写出正确结论的序号 .(把你认为正确结论的序号都填上)
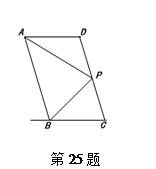
25.如图,已知AD‖BC,AP平分∠BAD,BP平分∠ABC,点P恰好在DC上,下面结论:①AP⊥BP,②点P到直线AD,BC的距离相等,③PD=PC其中结论正确的是
26.
 如图所示的正方形网格中,网格线的交点称为格点.已知
如图所示的正方形网格中,网格线的交点称为格点.已知 、
、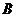 是两格点,如果
是两格点,如果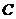 也是图中的格点,且使得
也是图中的格点,且使得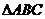 为等腰三角形,则点
为等腰三角形,则点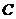 的个数有________ 个.
的个数有________ 个.
27. 若一个三角形的边长分别是12、16和20,则这个三角形最长边上的高长是_______。
28.有一直角三角形,其两边分别为12和16,则三角形的第三边是 。
29.填入两个和为6的无理数,使等式成立: + =6。
30.大于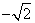 ,小于
,小于 的整数有______个。
的整数有______个。
31.如图,已知在 中,
中,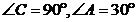 ,在直线
,在直线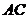 上找点
上找点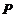 ,使
,使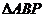 是等腰三角形,则
是等腰三角形,则 的度数为
.
的度数为
.
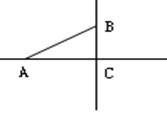
32.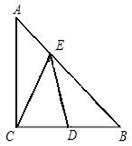 如图,在△
如图,在△
 中,
中, ,∠
,∠ 90°,
90°,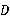 是
是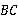 边的中点,
边的中点,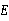 是
是 边上一动点,则
边上一动点,则
 的最小值是__________
的最小值是__________ _____.
_____.
33 .过点(﹣1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线
.过点(﹣1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线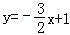 平行.则在线段AB上,横、纵坐标都是整数的点的坐标是
.
平行.则在线段AB上,横、纵坐标都是整数的点的坐标是
.
34.若函数y=4x+b的图象与两坐标轴围成的三角形面积为 ,那么b= .
,那么b= .
35.函数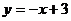 的图象在一、二象限部分的
的图象在一、二象限部分的 的取值范围是
的取值范围是
36. 如图36,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=18°,则∠CEF=________.
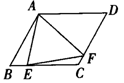
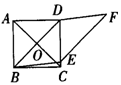

(36) (37) (38)
37.如图37,四边形ABCD是正方形,对角线AC、BD相交于O,四边形BEFD是菱形,若正方形的边长为6,则菱形的面积为________.
38.如图38,ABCD是正方形,E为BF上一点,四边形AFEC恰是一个菱形,则∠EAB=________.
39.如图39,矩形纸片ABCD中,AB=3cm,BC=4cm,现将A、C重合,使纸片折叠压平,设折痕为EF,试确定重叠部分的△AEF的面积是__________.

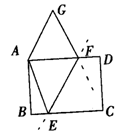

(39) (40) (41)
40.如图40所示,把一张长方形的纸条ABCD沿对角线BD将△BCD折成△BDF,DF交AB于E,若已知AE=2cm,∠BDC=30°,求纸条的长和宽各是________.
41. 如图41,ABCD为正方形,E是CF上一点,若DBEF是菱形,则∠EBC的度数_____________.
如图41,ABCD为正方形,E是CF上一点,若DBEF是菱形,则∠EBC的度数_____________.
42.如图,若△ABC的边AB=2,AC=3,Ⅰ、Ⅱ、Ⅲ分别表示以AB、BC、AC为边的正方形,则图中三个阴影部分面积之和为________。
43.在菱形ABCD中,对角线AC,BD交于点O,∠ABC=120°,周长为16,则OD=__________________
44.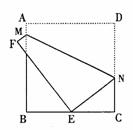 若一个平行四边形的一条边长为9厘米,一条对角线长为6厘米,则它的另一条对角线长m的取值范围是 .
若一个平行四边形的一条边长为9厘米,一条对角线长为6厘米,则它的另一条对角线长m的取值范围是 .
45.等腰三角形的两条中位线长分别是3和4,则它的周长是____________.
46.如图,将边长为8cm的正方形纸片ABCD折叠,
使点D落在BC边中点E处,点A落在点F处,
折痕为MN,则线段MN的长是________.
47.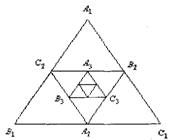 小明作出了边长为2的第1个正△A1B1C1,算出了正△A1B1C1的面积;
小明作出了边长为2的第1个正△A1B1C1,算出了正△A1B1C1的面积;
然后分别取△A1B1C1的三边中点A2、B2、C2,作出了第2个 正△A2B2C2,
正△A2B2C2,
算出了正△A2B2C2的面积。用同样的方法,作出了第3个正△A3B3C3,
算出了正△A3B3C3的面积……,由此可得,
第10个正△A10B10C10的面积是 。
48.在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE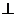 AB于E,PF
AB于E,PF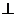 AC于F,M为EF的中点,则AM的最小值为______
AC于F,M为EF的中点,则AM的最小值为______
49.一个正方形的周长与一个等腰三角形的周长相等,若等腰三角形的两边长为4 和10
和10 ,则这个正方形的对角线长为_________
,则这个正方形的对角线长为_________
50.已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE',则EE'的长等于______.
51. 如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同 一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
52.如图,D、E分别在AB,AC上,BD=CE,BE,CD的中点分别是M,N,直线MN 分别交AB,AC于P,Q.
分别交AB,AC于P,Q.
 求证:AP=AQ
求证:AP=AQ
53.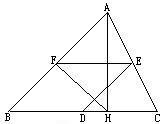 在△ABC中,AH⊥BC于H,D,E,F分别是BC,CA,AB的中点.
在△ABC中,AH⊥BC于H,D,E,F分别是BC,CA,AB的中点.
求证:∠DEF=∠HFE.
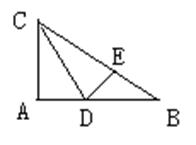
54.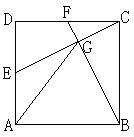 如图,在正方形ABCD中,取AD、CD边的中点E、F,连接CE、BF交于点G,连接AG。试判断AG与AB是否相等,并说明道理。
如图,在正方形ABCD中,取AD、CD边的中点E、F,连接CE、BF交于点G,连接AG。试判断AG与AB是否相等,并说明道理。
55.已知在 ABCD中,点E、F分别在AB、AD上。
ABCD中,点E、F分别在AB、AD上。
(1)若AB=10,AB与CD间距离为8,AE=BE,BF=FC,求△DEF的面积;
(2)若△ADE、△BEF、△CDF的面积分别为5、3、4,求△DEF的面积。
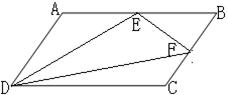
56. ABCD中,有一点P,使∠APD=∠ADP。连接AP、BP、DP、CP,求证∠PAD=∠PCB
ABCD中,有一点P,使∠APD=∠ADP。连接AP、BP、DP、CP,求证∠PAD=∠PCB 。
。

57.平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.
求证:∠DPA=∠DPC.

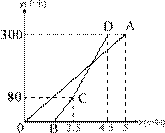
58.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间与轿车相遇。
59.某个体户购进一批时令水果,20天销售完毕.他将本次销 售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
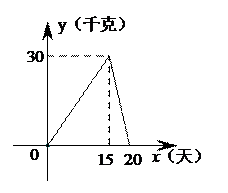 (3)若日销售量不
(3)若日销售量不 低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
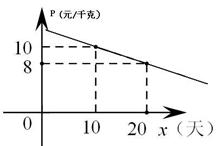
图甲 图乙
60.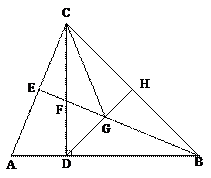 如图,在△ABC中,AB=BC,CD⊥AB于点D, CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG [来.
如图,在△ABC中,AB=BC,CD⊥AB于点D, CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG [来.
(1)求证:△ADC≌△FDB;
(2)求证:CE= BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
61.如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.(1)求证:AE=AF; (2)求证:CD=2BE+DE.
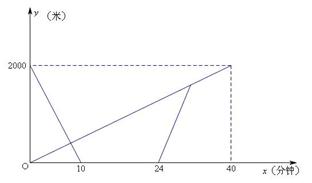
62.运动会前夕,小明和小亮相约晨练跑步.小明比小亮早1分钟离开家门,3分钟后迎面 遇到从家跑来的小亮.两人沿滨江路并行跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.下图是两人之间的距离y(米)与小明离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
遇到从家跑来的小亮.两人沿滨江路并行跑了2分钟后,决定进行长跑比赛,比赛时小明的速度始终是180米/分,小亮的速度始终是220米/分.下图是两人之间的距离y(米)与小明离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
⑴请直接写出小明和小亮比赛前的速度.
⑵请在图中的( )内填上正确的值,并求两人比赛过程中y与x之间的函数关系式.(不用写自变量x的取值范围)
⑶若小亮从家出门跑了14分钟后,按原路以比赛时的速度返回,则再经过多少分钟两人相遇?

63. 已知∠AOB=90º,在∠AOB的平分线OM上有一点C,OC= ,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.

(1)当三角板绕点C旋转到CD与OA垂直时(如图1),求证:OD+OE=2.
(2)当三角板绕点C旋转到CD与OA不垂直时:
①在图2这种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD,OE之间又有怎样的数量关系?请写出你的猜想,并给予证明.
②在图3这种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,
线段OD,OE之间又有怎样的数量关系?请直接写出你的猜想,并给予证明
64. 如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.
(1)在图1中,DE交AB于点M,DF交BC于点N.①证明DM=DN;②在这一过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的;若不发生变化,求出其面积;
(2)继续旋转直角三角板DEF至如图2的位置,延长AB交DE于点M,延长BC交DF于点N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

65.(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分 别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分 别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
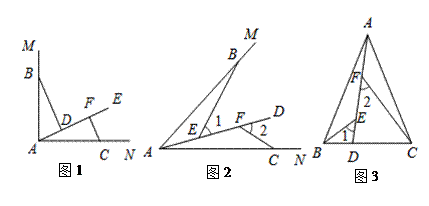 (3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.

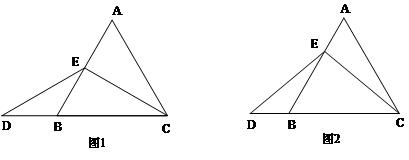
67.在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
试探索以下问题:
(1)当点E为AB的中点时,如图1,请判断线段AE与DB的大小关系,
请你直接写出结论:AE ▲ DB(填“>”“<”或“=”).
(2)当点E为AB上任意一点时,如图2,AE与DB的大小关系会改变吗?请说明理由.
68. 已知雅关服装厂有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装共70套,已知做一套M型号的时装需用A种布料0.6m,B种布料0.9m,可获利润45元;做一套N型号的时装需用A种布料1.1m,B种布料0.4m,可获利润50元,若生产N型号的时装x套,用这批布料生产这两种型号的时装所获的总利润为y元。 (1)求y(元)与x(套)之间的函数关系式,并求自变量x的取值范围; (2)雅关服装厂在生产这批时装时,当N型号的时装为多少套时,所获总利润最大。
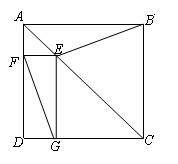
69. 如图,四边形ABCD是正方形,点E是AC上的点EG⊥DC,EF⊥AD,
(1)试猜测BE与FG关系如何?并说明理由.
(2)如果正方形ABCD的边长为4㎝,求四边形DGEF的周长
70. 矩形ABCD中,AC、BD相交于O,AE平分∠BAD交BC于E.
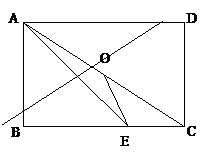 若∠CAE=15°,求∠BOE的度数.
若∠CAE=15°,求∠BOE的度数.
71.将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展平纸片(如图①);再次折叠该三角形纸片,使得点A与点D重合,折痕为EF,再次展平后连接DE、DF(如图②),试说明四边形AEDF是菱形.

72. 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
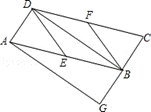
73.如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?
 若不变请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
若不变请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.
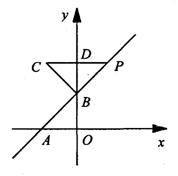
74.如图,一次函数y=x+1的图象与x轴交于点A,与y轴交于点B,点P位于第一象限且在直线AB上,以PB为一条直角边作一个等腰直角三角形PBC,其中C点位于直线AB的左上方,B点为直角顶点,PC与y轴交于点D.若△PBC与△AOB的面积相等,试求点P的坐标.
76. 如图,在平面直角坐标系,A(a,0),B(b,0),C(﹣1,2),且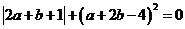 .
.
(1)求a,b的值;
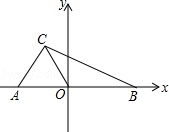 (2)在x轴的正半轴上存在一点M,使S△COM =
(2)在x轴的正半轴上存在一点M,使S△COM =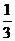 S△ABC,求出点M的坐标;
S△ABC,求出点M的坐标;
77.如图,直线y= x+8分别交x轴、y轴于A、B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)求证:AB、CD互相平分;
 (2)动点P从A出发,以每秒2个单位长度的速度,沿AO、OC向点C作匀速运动.设点P
(2)动点P从A出发,以每秒2个单位长度的速度,沿AO、OC向点C作匀速运动.设点P 的运动时间为t秒.在动点P从A出发的同时,动点Q 从C出发,以每秒1个单位长度的速度,沿CM向点M作匀速运动.当P、Q中的一点到达终点后,该点停止运动,另一点继续运动,直至到达终点,整个运动停止.问:是否存在这样的t,使得直线PQ将四边形AOCM的面积分成1∶2两部分?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
的运动时间为t秒.在动点P从A出发的同时,动点Q 从C出发,以每秒1个单位长度的速度,沿CM向点M作匀速运动.当P、Q中的一点到达终点后,该点停止运动,另一点继续运动,直至到达终点,整个运动停止.问:是否存在这样的t,使得直线PQ将四边形AOCM的面积分成1∶2两部分?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.


78. 如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA,求∠DAE的度数;

(2)如果把第(1)题中“AB=AC”的条件舍去,其余条件不变,那么∠DAE的度数会改变吗?请说明理由。
(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°” ,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系?
79. 如图,直线y=kx-1与x轴、y轴分别交与B、C两点,OC=2OB,点A是直线BC上一动点。
求B点的坐标和k的值;
若点A (x,y)在第一象限.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(x,y)在第一象限.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
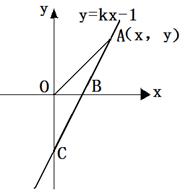 当点A运动到什么位置时,△AOB的面积是
当点A运动到什么位置时,△AOB的面积是 ;
;
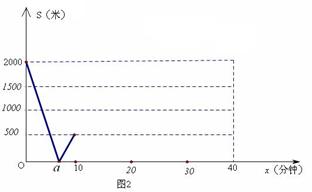
80.甲、乙两地之间有一条笔直的公路l,小明从甲地出发沿公路l步行前往乙地,同时小亮从乙出发沿公路l骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地。设小明与甲地的距离为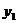 米,小亮与甲地的距离为
米,小亮与甲地的距离为 米,小明与小亮之间的距离为
米,小明与小亮之间的距离为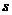 米,小明行走的时间为
米,小明行走的时间为 分钟,
分钟,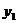 、
、 与
与 之间的函数关系如图1所示,
之间的函数关系如图1所示,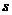 与
与 之间的函数如图2所示.
之间的函数如图2所示.
(1)小明与小亮第二次相遇是在出发后 分钟,相遇地距乙地 米;
(2)在图2中,补全整个过程中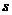 (米)与
(米)与 (分钟)之间的函数如图,并确定a的值。
(分钟)之间的函数如图,并确定a的值。
(3)求小亮从甲地返回到与小明相遇的过程中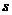 (米)与
(米)与 (分钟)之间的函数关系式;
(分钟)之间的函数关系式;