
1.下列各式中,运算正确的是 ( )
A. B.-=9 C.
B.-=9 C.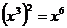 D.
D. =
=
2.下列图案中 ,既是中心对称又是轴对称图形的个数有 ( )

A.1个 B.2个 C.3个 D.4个
3.如图,在⊙O中,弦AB∥CD,若∠ABC= 40°,则∠BOD=
( )
40°,则∠BOD=
( )
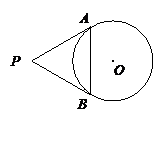 A.20° B.40° C.50° D.80°
A.20° B.40° C.50° D.80°

第3题图 第4题图
4.如图,从圆 外一点
外一点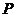 引圆
引圆 的两条切线
的两条切线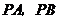 ,切点分别为
,切点分别为 .如果
.如果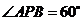 ,
, ,那么弦
,那么弦 的长是 ( )
的长是 ( )
A.4
B.8 C.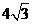 D.
D.
5.给出下列四个结论:①菱形的四个顶点在同一个圆上;②正多边形都是中心对称图形;
③三角形的外心到三个顶点的距离相等;④若圆心到直线上一点的距离恰好等于圆的半
径,则该直线是圆的切线.其中正确结论的个数有 ( )
A.1个 B.2个 C.3个 D.4个
6. 如图,在△ABC中,∠C=90°,AC=BC=4,
如图,在△ABC中,∠C=90°,AC=BC=4,
D是AB的中点,经过C、D两点的圆交AC、
BC于点E、F,且AE=CF.当圆变化时,点
C到线段EF的最大距离为 ( )
A. B.2 C.
B.2 C.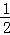
 D.2
D.2
7.分解因式: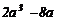 = .
= .
8.H7N9禽流感病毒颗粒有多种形状,其中球形直径约为0.0000001 m.将0.0000001用科学记数法表示为 .
9.某机械厂七月份生产零件50万个,第三季度生产零件196万个,设该厂 八、九月份平均每月的增长率为x,则可列方程为 .
八、九月份平均每月的增长率为x,则可列方程为 .
10.若3x=2y,则= .
11.已知x=1是一元二次方程 的一个根,则
的一个根,则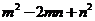 的值为 .
的值为 .
12. 如图,直线
如图,直线 与双曲线
与双曲线 交于A、B
交于A、B
两点,其横坐标分别为1和5,则不等式 的解集是
的解集是
.
13.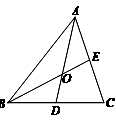 如图,若O为△ABC的两条中线AD和BE的交点,则S△BOD∶S△BEC
如图,若O为△ABC的两条中线AD和BE的交点,则S△BOD∶S△BEC
= .
14.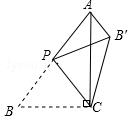 如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边
如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边
上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,
得到△B′CP,连接B′A ,则B′A长度的最小值是 .
,则B′A长度的最小值是 .

15.如图,一块直角三角板ABC的斜边AB与量角器的 直径恰
直径恰
好重合,点D 对应的刻度是58°,则∠ACD的度数为
对应的刻度是58°,则∠ACD的度数为
.
16.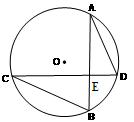 如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则
如图,⊙O中,弦AB⊥CD于E,若已知AD=6,BC=8,则
⊙O的半径为 .
17.(本题8分)
(1)计算: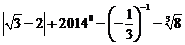 (2)解方程:x2-4x-99=0
(2)解方程:x2-4x-99=0
18.(本题8分)先化简再求值:
 ,其中
,其中 是不等式组
是不等式组 的一个整数解.
的一个整数解.
19.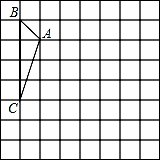 (本题10分)如图,方格纸中的每个小方格都是
(本题10分)如图,方格纸中的每个小方格都是 边长为
边长为
1个单位长度的正方形,每个小正方形的顶点叫格点,
△ABC的顶点均在格点上,请按要求完成下列步骤:画
出将△ABC向右平移3个单位后得到的△A1B1C1,再画
出将△A1B1C1绕点B1按逆时针方向旋转90 °后所得到的
°后所得到的
△A2B1C2.
20.(本题10分)为彰显学校“5+2”素质教 育特色,某校开设了书法、绘画、舞蹈三门
育特色,某校开设了书法、绘画、舞蹈三门
兴趣课程,现随机抽取了部分学生,了解他们对这三门课程的喜爱程度(每人从中只
能选一门),并将调查结果绘制成如下两幅统计图,请根据图中信息解答问题:
|
|||
|
|||
|
|
|
|
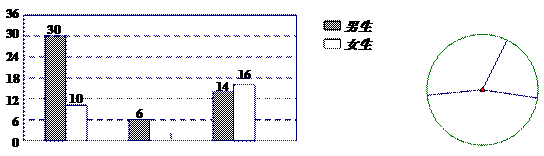
(1)请计算该样本中女生喜爱舞蹈的人数,并将条形统计图补 充完整;
充完整;
(2)本次抽样调查的样本容量是多少?
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢绘画的有多少人?
21.(本题10分)已知关于x的一元二次方程x2-(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若周长为16的等腰△ABC的两边AB,AC的长是 方程的两个实数根,求k的值.
方程的两个实数根,求k的值.
22. (本题10分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬
(本题10分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬
衫,面市后果然供不应求,商家又用28800元够进了第二批这种衬衫,所购数量是第
一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部
 售完利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
售完利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
23. (本题10分)如图所示,E是正方形
(本题10分)如图所示,E是正方形 ABCD的边AB上的动
ABCD的边AB上的动
点,正方形的边长为4,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)AE=x,B F=y.当x取什么值时,y有最大值?并求出
F=y.当x取什么值时,y有最大值?并求出
这个最大值.
24. (本题10分)如图,在平面坐标系中,∠AOB=90°,
(本题10分)如图,在平面坐标系中,∠AOB=90°,
AB∥x轴,OB=2,双曲线y=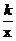 经过点B.将△AOB
经过点B.将△AOB
绕点B逆时针旋转,使点O的对应点D落在X轴的
正半轴上.若AB的对应线段CB恰好经过点O.
(1)点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
25. (本题12分)已知如图
(本题12分)已知如图 ,AB为⊙O的直径,C为⊙O上的一
,AB为⊙O的直径,C为⊙O上的一
点且AC=4,BC=8,以BC为底边作等腰直角△BCD,边 CD
CD
交⊙O于E.
(1)求AE的长和⊙O的半径;
(2)求证CE=ED.

26.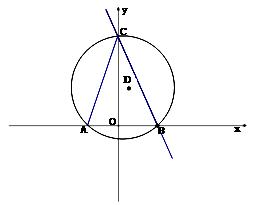 (本题14分)已知,如图在平面直角坐标系中,
(本题14分)已知,如图在平面直角坐标系中,
A(-2,0),B(3,0),直线l:y=kx+b经
过B点,与y轴的正半轴交于C点,连接AC,
此时∠ACB=45°.有一⊙D经过△ABC的三个
顶点.
(1)求⊙D 的圆心D的坐标;
的圆心D的坐标;
(2)求直线l解析式;
(3)直接写出直角△AOC的内切圆的半径的长.