
1、若两个球的表面积之比为 ,则这两个球的体积之比为
,则这两个球的体积之比为
A.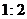 B.
B. C.
C. D.
D.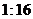
2、1.已知m是平面α的一条斜线,点A∉α,l为过点A的一条动直线,那么下列情形可能出现的是 A.l∥m,l⊥α B.l⊥m,l⊥α C.l⊥m,l∥α
D.l∥m,l∥α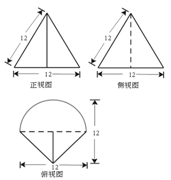
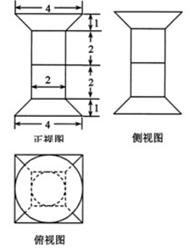
3、如图是某简单组合体的三视图,则该组合体的体积为 ( )
A.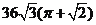 B.
B. C.
C.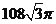 D.
D.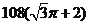
4. 已知直线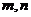 互不重合,平面
互不重合,平面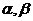 互不重合,下列命题正确的是
互不重合,下列命题正确的是
A 、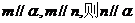 B、
B、
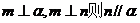
C、 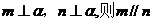 D、
D、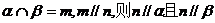
5、 如图,长方体
如图,长方体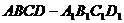 中,
中,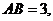
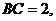
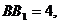 E为AD的中点,点P在线段
E为AD的中点,点P在线段
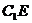 上,则点P到直
上,则点P到直
线BB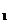 的距离的最小值为
的距离的最小值为

A.2
B.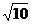 C.
C.
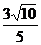 D.
D.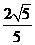
6、 某几何体的三视图如右图所示,则它的体积是
某几何体的三视图如右图所示,则它的体积是
(A)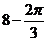 (B)
(B)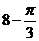 (C)
(C)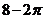 (D)
(D)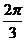
7.正六棱柱的底面边长为4,高为6,则它的外接球的表面积为
A. 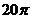 B.
B. 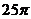 C.
C. 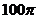 D.
D. 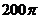
8、已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于
A.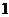 B.
B.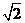 C.
C.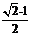 D.
D.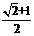
9、已知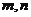 为异面直线,
为异面直线,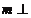 平面
平面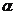 ,
,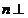 平面
平面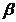 .直线
.直线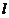 满足
满足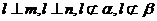 ,则
,则
A.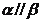 ,且
,且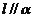 B.
B.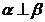 ,且
,且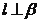
 C.
C.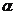 与
与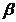 相交,且交线垂直于
相交,且交线垂直于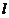 D.
D.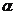 与
与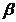 相交,且交线平行于
相交,且交线平行于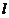
10、一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为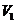 ,
,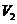 ,
,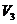 ,
,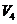 ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有 ( )
,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有 ( )
A.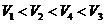 B.
B.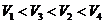
C.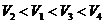 D.
D.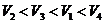
11、 已知三棱锥
已知三棱锥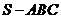 中,底面
中,底面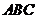 为边长等于2的等边三角形,
为边长等于2的等边三角形,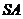
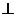 底面
底面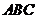 ,
,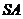
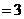 ,那么直线
,那么直线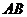 与平面
与平面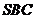 所成角的正弦值为
所成角的正弦值为
A.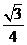 B.
B.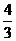 C.
C.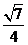 D.
D.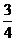
12、如图, 在长方体ABCD-A1B1C1D1中,对角线B1D与平面A1BC1相交于点E,则点E为△A1BC1的
A.垂心 B.内心 C.外心 D.重心
13、 若一个圆锥的侧面展开图恰好是一个半圆,则这个圆锥的侧面积与表面积之比为
若一个圆锥的侧面展开图恰好是一个半圆,则这个圆锥的侧面积与表面积之比为
14、如图,直三棱柱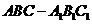 中,
中,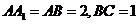 ,
,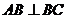 ,则该三棱柱的侧面积为
。
,则该三棱柱的侧面积为
。
15. 如图,平面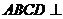 平面
平面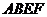 ,四边形
,四边形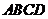 是正方形,四边形
是正方形,四边形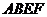 是矩形,且
是矩形,且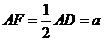 ,
,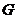 是
是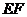 的中点,则
的中点,则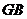 与平面
与平面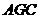 所成角的正弦值为___________。
所成角的正弦值为___________。
16.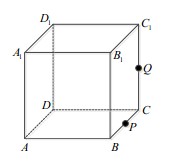 如图,正方体
如图,正方体 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段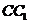 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_____(写出所有正确命题的编号).
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_____(写出所有正确命题的编号).
①当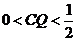 时,S为四边形;②当
时,S为四边形;②当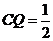 时,S为等腰梯形;
时,S为等腰梯形;
③当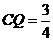 时,S与
时,S与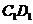 的交点R满足
的交点R满足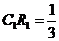 ;
;
④当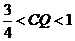 时,S为六边形; ⑤当
时,S为六边形; ⑤当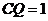 时,S的面积为
时,S的面积为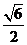 .
.
17.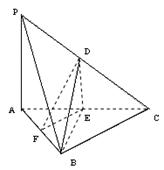 如图,在三棱锥P
如图,在三棱锥P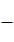 ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.
ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
18.如图,已知四边形ABCD为矩形,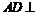 平面ABE,AE=EB=BC=2,F为CE上的点,且
平面ABE,AE=EB=BC=2,F为CE上的点,且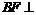 平面ACE.
平面ACE.
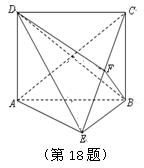 (I)求证:AE//平面BDF;
(I)求证:AE//平面BDF;
(II)求三棱锥D-ACE的体积.
19.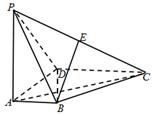 如图,在四棱锥
如图,在四棱锥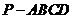 中,
中,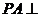 底面
底面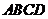 ,
,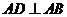 ,
,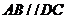 ,
,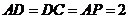 ,
,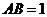 ,点
,点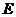 为棱
为棱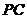 的中点.
的中点.
⑴证明: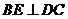 ;
;
⑵求直线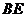 与平面
与平面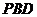 所成角的正弦值;
所成角的正弦值;
20.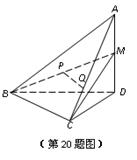 如图,在四面体
如图,在四面体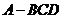 中,
中,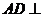 平面
平面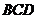 ,
,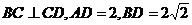 .
.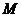 是
是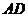 的中点,
的中点,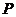 是
是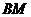 的中点,点
的中点,点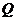 在线段
在线段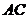 上,且
上,且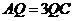 .
.
(1)证明: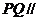 平面
平面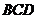 ;
;
(2)若二面角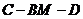 的大小为
的大小为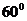 ,求
,求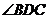 的大小.
的大小.
21.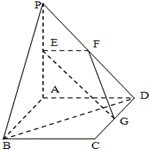 平面
平面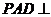 平面
平面 ,
, 为正方形,
为正方形,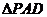 是直角三角形,且
是直角三角形,且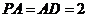 ,
,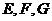 分别是线段
分别是线段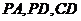 的中点
的中点
(1)求证: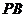 //平面
//平面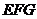 ;
;
(2)在线段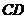 上是否存在一点
上是否存在一点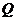 ,使得点
,使得点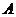 到平面
到平面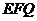 的距离为
的距离为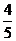 ,若存在,求出
,若存在,求出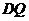 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
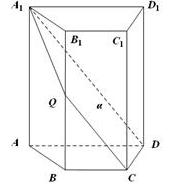
22.如图,四棱柱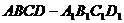 中,
中,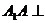 底面
底面 .四边形
.四边形 为梯形,
为梯形,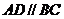 ,且
,且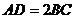 .过
.过 三点的平面记为
三点的平面记为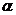 ,
,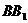 与
与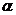 的交点为
的交点为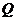 .
.
(Ⅰ)证明: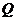 为
为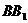 的中点;
的中点;
 (Ⅱ)求此四棱柱被平面
(Ⅱ)求此四棱柱被平面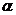 所分成上下两部分的体积之比;
所分成上下两部分的体积之比;
(Ⅲ)若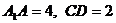 ,梯形
,梯形 的面积为
的面积为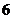 ,求平面
,求平面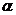 与底面
与底面 所成二面角大小.
所成二面角大小.