1．用符号表示“点A在直线l上，l在平面α外”正确的是( )
A．A∈l，l⊄α B．A∈l，l∉α
C．A⊂l，l∉α D．A⊂l，l⊄α
2．下列说法中正确的是( )
A．棱柱的侧面可以是三角形
B．正方体和长方体都是特殊的四棱柱
C．所有的几何体的表面都能展成平面图形
D．棱柱的各条棱都相等
3．已知三棱锥的正视图与俯视图如图所示，俯视图是边长为2的正三角形，则该三棱锥的侧视图可能为( )
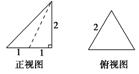
4．已知水平放置的△ABC是按“斜二测画法”得到如右图所示的直观图，其中B′O′＝C′O′＝1，A′O′＝，那么原△ABC是一个( )
A．等边三角形 B．直角三角形
C．三边中有两边相等的等腰三角形 D．三边互不相等的三角形
5．在空间四边形
各边
上分别取
四点，如果与
能相交于点
，那么( )
A.点必在直线
上 B.点必在直线
上
C.点必在平面
内
D.点必在平面外
6．把两半径为2的铁球熔化成一个球，则这个大球的半径应为( )
A
4 B 
C
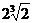D
7．棱台上、下底面面积之比为1∶9,则棱台的中截面分棱台成两部分的体积之比是( )
A1∶7 B2∶7 C7∶19 D5∶ 16
8．a，b，c表示直线，M表示平面，给出下列四个命题：①若a∥M，b∥M，则a∥b；②若b
M，a∥b，则a∥M；③若a⊥c，b⊥c，则a∥b；④若a⊥M，b⊥M，则a∥b.其中正确命题的个数有( )
A．0个 B．1个 C．．2个 D．3个
9．在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是( )
A．
B．
C．
D．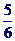
10．在正方体ABCD－A′B′C′D′中，过对角线BD′的一个平面交AA′于E、交CC′于F，则以下结论中错误的是( )
A．四边形BFD′E一定是平行四边形
B．四边形BFD′E有可能是菱形
C．四边形BFD′E有可能是正方形
D．四边形BFD′E在底面投影一定是正方形
11．圆柱被一个平面截去一部分后与半球(半径为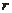
)组成一个几何体，该几何体的三视图中的正视图和俯视图如右图所示，若该几何体的表面积为
，则
( )
(A)
(B)
(C)
(D)
12．如右图1，在透明密封的长方体ABCD－A1B1C1D1容器内已灌进一些水，固定容器底面一边BC于水平的地面上，再将容器倾斜，随着倾斜度的变化，有下列四个命题：
①有水的部分始终呈棱柱形；
②水面四边形EFGH的面积不会改变；
③棱A1D1始终与水面EFGH平行；
④当点E、F分别在棱BA、BB1上移动时(如图2)，BE.BF是定值．
其中正确命题的序号是( )
A．①②③ B．①②
C．③④ D．①③④
第Ⅱ卷(非选择题：共90分)
13．某几何体的三视图如图所示(单位：
)，则该几何体的体积是_________
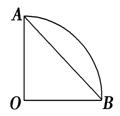
14．如图所示，扇形所含的中心角为90°，弦AB将扇形分成两个部分，这两部
分各以AO为轴旋转一周，所得的旋转体体积V1和V2之比为________
15．圆柱的轴截面是边长为5的正方形ABCD,圆柱侧面上从A到C的最短距离为________
16．
如图，在四棱柱A1B1C1 D1－ABCD中，侧棱垂直底面，当底面四边形ABCD满足条件_______时，有A1
B⊥B1 D1．(注：填上你认为正确的一种条件即可，不必考虑所有可能的情形.)
|
|
|
17．(本小题满分10分)圆柱的高是8cm，表面积是130πcm2，求它的底面圆半径和体积．
18．
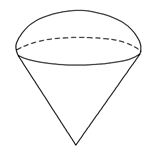(本小题满分12分)某甜品店制作一种蛋筒冰淇淋，其上半部分呈半球形、下半部分呈圆锥形(如图)．现把半径为10cm的圆形蛋皮等分成5个扇形，用一个扇形蛋皮围成圆锥的侧面(蛋皮厚度忽略不计)，求该蛋筒冰淇淋的表面积和体积．
19．(本小题满分12分)如图所示的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出(单位：cm)．
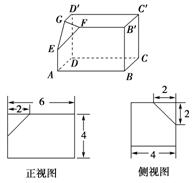(1)按照画三视图的要求画出该多面体的俯视图；
(2)按照给出的尺寸，求该多面体的体积；
(3)在所给直观图中连接BC′，求证：BC′∥面EFG.
20.
(本小题满分12分)如图,三棱柱
中,侧棱垂直底面,
∠ACB=90°,AC=BC=AA=1,D是棱AA1的中点.
(I)证明:平面
⊥平面
(Ⅱ)求三棱锥C-ABD的体积
21．
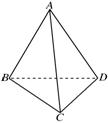(本小题满分12分)如图，四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．
(1)求证：BC⊥AD；
(2)试问该四面体的体积是否存在最大值？若存在，求出这个最大值及此时棱长AD的大小；若不存在，请说明理由．
22．
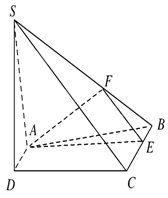(本小题满分12分)如图，在四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD＝90°，且BC＝2AD，AB＝4，SA＝3.
(1)求证：平面SBC⊥平面SAB；
(2)若E、F分别为线段BC、SB上的一点(端点除外)，满足＝＝λ.
①求证：不论λ为何值，都有SC∥平面AEF；②是否存在实数λ，使得△AEF为直角三角形，若存在，求出所有符合条件的λ值；若不存在，说明理由．