1．初中学过的三角形、长方形、正方形、平行四边形、梯形、圆等都是平面图形．

2．粉笔盒、铅笔盒、课桌腿、书本等都是立体图形．

3．空间几何体．

(1)空间中的物体都占据着空间的一部分，若只考虑物体的形状和大小，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体．

(2)多面体．

定义：由若干个平面多边形围成的几何体叫做多面体．围成多面体的各个多边形叫做多面体的面；相邻两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点．

多面体至少有几个面？几条棱？几个顶点？

答案：4个　6条　4个

4. 棱柱、棱锥、棱台的概念.

多面 体	定义	图形及表示	相关概念
棱柱	有两个互相平行，其余各面都是平行四边形，并且每相邻两个四边形的公共边都相互平行，由这些边所围成的多面体叫做棱柱	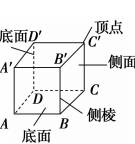如图可记作：棱柱AC′或ABCD A′B′C′D′	侧面：其余各面；侧棱：相邻侧面的公共边；顶点：侧面与底面的公共顶点

棱柱两底面全等且互相平行对吗？

答案：对

多面 体	定义	图形及表示	相关概念
棱锥	有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫棱锥	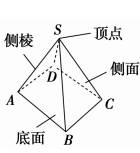如图可记作： 棱锥SABCD	底面(底)：多边形； 侧面：有公共顶点的各0个三角形；侧棱：相邻侧面的公共边； 顶点：各侧面的公共顶点

多面 体	定义	图形及表示	相关概念
棱台	用一个平行于底面的平面去截棱锥，底面与截面之间的部分叫做棱台	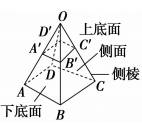如图可记作：棱台ABCDA′B′C′D′	上底面：原棱锥的截面；下底面：原棱锥的底面；侧面：其余各面；侧棱：相邻侧面的公共边；顶点：侧面与上(下)底面的公共顶点

三棱台有几个面？两底面形状和位置关系如何？

答案：5个面　两底面是相似三角形且互相平行

5．棱柱、棱锥、棱台的分类．

(1)棱柱的分类．

①按底面多边形的边数分类．

②按侧棱与底面是否垂直分类．

(2)棱锥的分类(棱台分类)．

①按底面多边形的边数分类．

三棱锥、四棱锥、五棱锥等．

②按底面多边形是否为正多边形分类．

正棱锥和一般棱锥．

1．三棱锥又称四面体，则在四面体A­BCD中，可以当作棱锥底面的三角形有(D)

A．1个　 B．2个　 C．3个　 D．4个

2．关于棱台，下列说法正确的是(D)

A．两底面可以不相似

B．侧面都是全等的梯形

C．侧棱长一定相等

D．侧棱延长后交于一点

解析：只有D符合棱台的特征．

3．下列图形经过折叠可以围成一个棱柱的是(D)

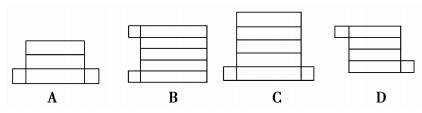
解析：A、B、C中底面多边形的边数与侧面数不相等．

1．下列说法正确的是(D)

A．有两个面平行，其余各面都是四边形的几何体叫棱柱

B．有两个面平行，其余各面都是平行四边形的几何体叫棱柱

C．各侧面都是正方形的四棱柱一定是正方体

D．九棱柱有9条侧棱，9个侧面，侧面为平行四边形

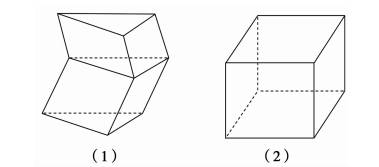
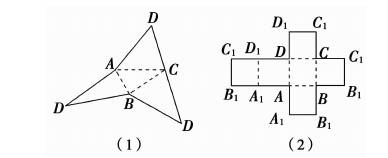
解析：A、B都错，反例如图(1)；C也错，反例如图(2)，上、下底面是全等的菱形，各侧面是全等的正方形，它不是正方体；根据棱柱的定义，知D对．

2．如图所示是一个正方体，它的展开图可能是下面四个展开图中的(A)

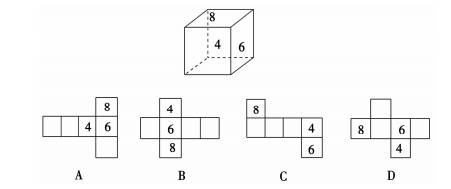
解析：由所给正方体可知，4，6，8分别位于相邻的三个侧面，故选A.

3．八棱锥的侧面个数是(A)

A．8个　 B．9个　 C．10个　 D．11个

解析：底面为8边形，须有8个侧面．

4．下列说法中正确的是(B)

A．所有的棱柱都有一个底面

B．棱柱的顶点至少有6个

C．棱柱的侧棱至少有4条

D．棱柱的棱至少有4条

解析：A错，两个底面；B正确，最简单的是三棱柱．

5．如果一个棱锥的各个侧面是等边三角形，那么这个棱锥不可能是(D)

A．三棱锥　 B．四棱锥

C．五棱锥　 D．六棱锥

解析：若是六棱锥，各侧面顶角之和为6×60°＝360°，即各侧面就成为平面图形．

6．一个棱柱至少有______个面，面数最少的棱柱，有______条棱，有______条侧棱，有______个顶点．

答案：5　9　3　6

7．如图，已知长方体ABCDA₁B₁C₁D₁，过BC和AD分别作一个平面交底面A₁B₁C₁D₁于EF、PQ，则长方体被分成的三个几何体中，棱柱的个数是________．

解析：三个几何体都是棱柱．

答案：3

8．一个棱柱有10个顶点，所有的侧棱长的和为60 cm，则每条侧棱长为________ cm.

解析：是五棱柱，侧棱长相等60÷5＝12.

答案：12

9．如图，模块①-⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成．现从模块①-⑤中选出三个放在模块⑥上，使得模块⑥成为一个棱长为3的大正方体．则下列选择模块中，能够完成任务的为________．

解析：先补齐中间一层只能用模块⑤，然后再用模块①②组合后补上面一层．

答案：①②⑤

10．以三棱台的顶点为三棱锥的顶点，这样可以把一个三棱台分成________个三棱锥．

解析：如图，分割为A₁ABC，BA₁B₁C₁，CA₁B₁B 3个棱锥．

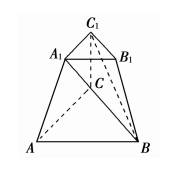
答案：3

11．请画出如图所示的几何体的表面展开图．

解析：展开图如图所示．

12．在正四棱柱上任意选择4个顶点，试画图分析以下两个问题：

(1)这4个顶点可能是哪几种平面图形的顶点？

(2)这4个顶点可能是哪几种空间图形的顶点？

答案：(1)这4个顶点可能是以下平面图形的顶点：矩形；正方形．

(2)这4个顶点可能是以下空间图形的顶点：

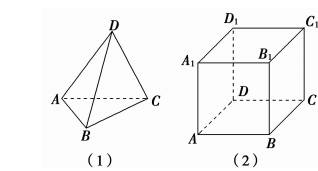
有一个面为等腰三角形其余面是直角三角形的四面体(如图1、2)；每个面都是等腰三角形的四面体(如图3)；每个面都是直角三角形的四面体(如图4)．

13．长方体ABCDA₁B₁C₁D₁中，AB＝4，BC＝3，BB₁＝5，一只蚂蚁从点A出发沿表面爬行到点C₁，求蚂蚁爬行的最短路线．

解析：沿长方体的一条棱剪开，使A和C₁展在同一平面上，求线段AC₁的长即可，有如图所示的三种剪法：

(1)若将C₁D₁剪开，使面AB₁与面A₁C₁共面，可求得AC₁＝＝＝4.

(2)若将AD剪开，使面AC与面BC₁共面，可求得

AC₁＝＝＝3.

(3)若将CC₁剪开，使面BC₁与面AB₁共面，可求得

AC₁＝＝.

比较可得蚂蚁爬行的最短路线长为.

1．对棱柱的判断．

(1)有两个面相互平行；

(2)其余各面是平行四边形；

(3)这些平行四边形的面中，每相邻两个面的公共边都互相平行．这三个条件缺一不可．

2．对棱锥的判断．

强调各侧面三角形必须有一个公共顶点．

3．对棱台的判断．

(1)棱台的上、下底面平行；

(2)延长棱台的各侧棱交于一点；

(3)棱台的各侧面都是梯形．三者缺一不可．

4．棱柱概念的推广．

(1)斜棱柱：侧棱不垂直于底面的棱柱叫斜棱柱．

(2)直棱柱：侧棱垂直与底面的棱柱叫直棱柱．

(3)正棱柱：底面是正多边形的直棱柱叫正棱柱．

(4)平行六面体：底面是平行四边形的四棱柱叫平行六面体，即平行六面体的六个面都是平行四边形．

(5)长方体：底面是矩形的直平行六面体叫长方体．

(6)正方体：棱长都相等的长方体叫正方体.