
1.
不等式 恒成立的充分条件是
恒成立的充分条件是 ,则实数
,则实数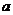 的取值范围是 _ .
的取值范围是 _ .
2.
不等式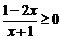 的解集是 ___________________
的解集是 ___________________

3. 如图在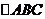 中,
中, ,
,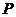
为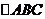 所在平面外一点,
所在平面外一点, 平面
平面 ,
, ,
,
则点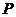 到直线
到直线 的距离为:________________
的距离为:________________

4.正方体的全面积是 ,它的顶点都在一个球面上,则这个球的表面积为________
,它的顶点都在一个球面上,则这个球的表面积为________
5.
圆柱的轴截面为边长为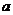 的正方形,则此圆柱的全面积为______________
的正方形,则此圆柱的全面积为______________
6.在体积为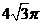 的球的表面上有
的球的表面上有 三点,
三点, 两点的球面距离为
两点的球面距离为 .则球心到平面
.则球心到平面 的距离为______________________.
的距离为______________________.
7.正三棱锥侧棱与底面所成角为 ,且
,且 则侧面和底面所成的二面角的大小为_____________
则侧面和底面所成的二面角的大小为_____________
8 .一圆锥侧面展开为半径为8的半圆,则此圆锥的体积为______________________
9. 地球的北纬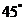 圈上有A,B两点,它们分别在东经
圈上有A,B两点,它们分别在东经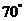 和东经
和东经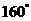 的经线上,则A,B两点的球面距离与其在此北纬
的经线上,则A,B两点的球面距离与其在此北纬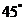 圈上劣弧长的比值为____________
圈上劣弧长的比值为____________
10.设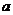 为实常数,
为实常数, 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,若
,若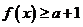 对一切
对一切 成立,则
成立,则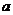 的取值范围为______________________.
的取值范围为______________________.
11. 是
是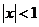 且
且 的
(
)
的
(
)
(A)充分非必要条件 (B)必要非充分条件 (C)充要条件 (D)既非充分又非必要
12.正四棱锥的侧棱长为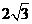 ,侧棱和底面所成角为
,侧棱和底面所成角为 ,则该棱锥的体积为
(
)
,则该棱锥的体积为
(
)
(A)3 (B)6 (C)9 (D) 18
13. 一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是 ( )
(A) 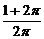 (B)
(B)
 (C)
(C) (D)
(D)
14. 长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是
(
)
长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E、F、G分别是DD1、AB、CC1的中点,则异面直线A1E与GF所成的角是
(
)
A.arccos B.
B. 
C.arccos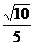 D.
D.
15.
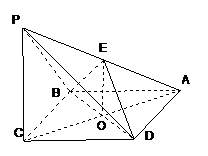
四棱锥 中,底面ABCD是边长为
中,底面ABCD是边长为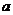 的菱形,
的菱形,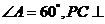 平面ABCD,
平面ABCD,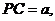 E为PA的中点,
E为PA的中点,
(1)
求证: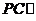 平面
平面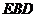 . (2)求E到平面PBC的距离
. (2)求E到平面PBC的距离
16.. 正四棱柱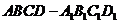 中,
中,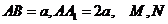 分别为
分别为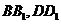 的中点。
的中点。
(1)求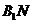 与平面
与平面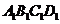 所成角的大小。
所成角的大小。
(2)求异面直线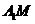 与
与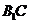 所成角的大小。
所成角的大小。
(3)若正四棱柱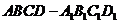 的体积为
的体积为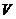 ,求三棱锥
,求三棱锥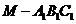 的体积。
的体积。

17. 如图:在三棱柱 中,四边形
中,四边形 是菱形,四边形
是菱形,四边形 是矩形,且
是矩形,且 .
.
(1).求证: 平面
平面 (2).若
(2).若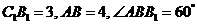 ,求
,求 与平面
与平面 所成角的大小
所成角的大小

18.某甜品店制作一种蛋筒冰激凌,其上部分是半球形,下半部分呈圆锥形(如图),现把半径为 的圆形蛋皮等分成
的圆形蛋皮等分成 个扇形,用一个蛋皮围成圆锥的侧面(蛋皮的厚度忽略不计),求该蛋筒冰激凌的表面积和体积(精确到
个扇形,用一个蛋皮围成圆锥的侧面(蛋皮的厚度忽略不计),求该蛋筒冰激凌的表面积和体积(精确到 )
)

19. 若函数 同时满足以下条件:
同时满足以下条件:
①它在定义域 上是单调函数;②存在区间
上是单调函数;②存在区间
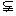
 使得
使得 在
在 上的值域也是
上的值域也是 ,我们将这样的函数称作“
,我们将这样的函数称作“ 类函数”。
类函数”。
(1)函数 是不是“
是不是“ 类函数”?如果是,试找出
类函数”?如果是,试找出 ;如果不是,试说明理由;
;如果不是,试说明理由;
(2)求使得函数 是“
是“ 类函数”的常数
类函数”的常数 的取值范围。
的取值范围。