|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
1.在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A.4cm  B.5cm C.9cm
D.13cm
B.5cm C.9cm
D.13cm
2. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
A.两点之间,线段最短
 B.垂线段最短
B.垂线段最短
 C.三角形具有稳定性
C.三角形具有稳定性
D.两直线平行,内错角相等
3.等腰 三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
A.7cm B.3cm C.7cm或3cm D.8cm
4.若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A.1 B.5 C.7 D.9
5.具备下列条件的三角形ABC中,不为直角三角形的是( )
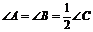
A.∠A+∠B=∠C B.
C.∠A=90°-∠B D.∠A-∠B=90°
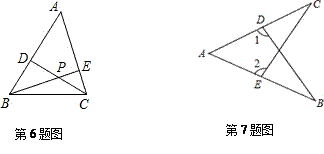
6.如图,在锐角△ABC中,CD,BE分别是AB,AC边上的高,且CD,BE相交于一点P,若∠A=50°,则∠BPC=( )
A.150° B.130° C.120° D.100°
姓名: 分数:
7.如图,∠B=∠C,则( )
A.∠1=∠2 B.∠1>∠2 C.∠1<∠2 D.不确定
8.若一个多边形的内角和为1080°,则这个多边形的边数为( )
A.6 B.7 C.8 D.9
9.在等腰三角形ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为1 5和12两部分,则这个等腰三角形的底边长为( )
5和12两部分,则这个等腰三角形的底边长为( )
A.7 B.7或11 C.11 D.7或10
10.如图,已知AB∥CD.则角α、β、γ之间关系为( )
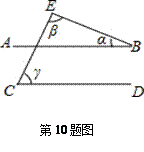 A.α+β+γ=180° B.α-β+γ=180°
A.α+β+γ=180° B.α-β+γ=180°
C.α+β-γ=180° D.α+β+γ=360°
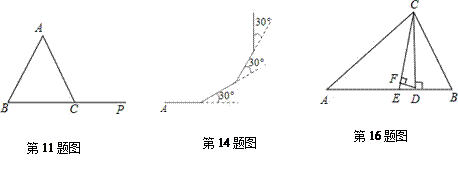
11.如图,P为△ABC中BC边的延长线上一点,∠A=50°,∠B=70°,则∠ACP= 度.
12.等腰三角形的两边长分别为4和9,则第三边长为
 13
13 .如果一个三角形两边为2cm,7cm,且三角形的第三边为奇数,则三角形的周长是
.如果一个三角形两边为2cm,7cm,且三角形的第三边为奇数,则三角形的周长是
 cm.
cm.
14.如图, 小亮从A点出发,沿直线前进100m后向左转30°,再沿直线前进100m,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了
m.
小亮从A点出发,沿直线前进100m后向左转30°,再沿直线前进100m,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了
m.
15.BM 是△ABC中AC边上的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长之差为
cm.
是△ABC中AC边上的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长之差为
cm.
16.如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF= 度.
17.(本题满分6分)一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
18.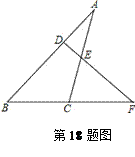 (本题满分8分)如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.
(本题满分8分)如图,点F是△ABC的边BC延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF的度数.
19.(本题满分8分)一个零件的形状如图,按规定∠A=90°,∠ABD和∠ACD,应分别是32 °和21°,检验工人量得∠BDC=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.
°和21°,检验工人量得∠BDC=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.

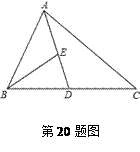
20.(本题满分10分)如图,AD是△ABC的中线,BE是△ABD的中线. (1)在△BED中作BD边上的高. (2)若△ABC的面积为20,BD=5,则点E到BC边的距离为多少?
21.(本题满分8分)如图,已知AB∥CD,试判断∠1、∠2和∠3的关系并说明理由;



22.(本题满分10分)
(1)如图(1),在△ABC中,∠C>∠B,AD⊥BC于点D,AE平分∠BAC,你能找出∠EAD与∠B、∠C之间的数量关系吗?并说明理由. (2)如图(2),AE平分∠BAC,F为AE上一点,FM⊥BC于点M,这时∠EFM与∠B、∠C之间又有何数量关系?请你直接说出它们的关系,不需要证明.

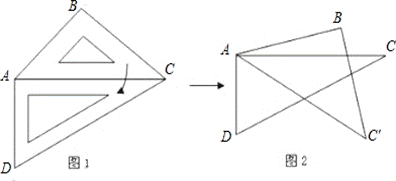
23.(本题满分10分)取一副三角板按图1拼接,固定三角板ADC,将三角板ABC绕点A依顺时针方向旋转一个大小为α的角(0°<α≤45°)得到△ABC′,如图所示.
试问:(1)当α为多少度时,能使得图2中AB∥DC;
(2)连接BD,当0°<α≤45°时,探寻∠DBC′+∠CAC′+∠BDC
 值的大小变化情况,并给出你的证明.
值的大小变化情况,并给出你的证明.


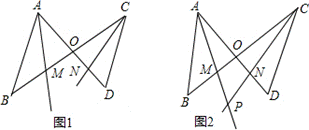
24. (本题满分12分)如图1,在同一平面内,四条线AB、BC、CD、DA首尾顺次相接,AD、BC相交于点O,AM、CN分别是∠BAD和∠BCD的平分线,∠B=α,∠D=β.
(1)如图2,AM、CN相交于点P.
①当α=β时,判断∠APC与α的大小关系,并说明理由.
②当α>β时,请直接写出∠APC与α,β的数量关系.
(2)是否存在AM∥CN的情况?若存在,请判断并说明α,β的数量关系;若不存在,请说明理由.
(本题满分12分)如图1,在同一平面内,四条线AB、BC、CD、DA首尾顺次相接,AD、BC相交于点O,AM、CN分别是∠BAD和∠BCD的平分线,∠B=α,∠D=β.
(1)如图2,AM、CN相交于点P.
①当α=β时,判断∠APC与α的大小关系,并说明理由.
②当α>β时,请直接写出∠APC与α,β的数量关系.
(2)是否存在AM∥CN的情况?若存在,请判断并说明α,β的数量关系;若不存在,请说明理由.