回忆：七年级时，我们在“展开与折叠”的学习活动中，已经知道圆锥的侧面展开图是一个扇形。那么怎样求圆锥的侧面展开图的面积呢？

　 二、探究学习

1．圆锥的基本概念：

连结圆锥的顶点S和底面圆上任意一点的线

段SA、SA₁……叫做圆锥的母线，

连接顶点S与底面圆的圆心O的线段叫做

圆锥的高。

2．圆锥中的各元素与它的侧面展开图——扇形的各元素之间的关系：

将圆锥的侧面沿母线l剪开，展开成平面图形，可以得到一个扇形，设圆锥的底面半径为r，这个扇形的半径等于什么？扇形弧长等于什么？

3．圆锥侧面积计算公式：

圆锥的母线即为扇形的半径，而圆锥

底面的周长是扇形的弧长，这样，

　 S_圆锥侧=S_扇形=.2πr . l = πrl

4．圆锥全面积计算公式

　 　S_圆锥全=S_圆锥侧+S_圆锥底面= πr l +πr ²=πr(l +r)

5.典型例题

例1：制作如图所示的圆锥形铁皮烟囱帽，其尺寸要求为：底面直径80cm,母线长50cm,求烟囱帽铁皮的面积(精确到1cm²)

例2：如图所示的扇形中，半径R=10，圆心角θ=144°用这个扇形围成一个圆锥的侧面.

(1)求这个圆锥的底面半径r;

(2)求这个圆锥的高(精确到0.1)

6.巩固练习

(1).圆锥的底面直径为80cm.母线长为90cm,求它的全面积.

(2).如图.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.

1、圆锥的侧面积公式与全面积公式；

2、圆锥中的各元素与它的侧面展开图——扇形的各元素之间的关系.

[课后作业]

1．圆锥母线长5 cm，底面半径为3 cm，那么它的侧面展形图的圆心角是…(　　 )

　　 A．180°　 B．200°　 C. 225°　 D．216°

2．若一个圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的圆心角是(　　 )

　　 A．180°　　 B. 90°

　　 C．120°　　 D．135°

3．在半径为50 cm的图形铁片上剪去一块扇形铁皮，用剩余部分制做成一个底面直径为80 cm，母线长为50 cm的圆锥形烟囱帽，则剪去的扇形的圆心角的度数为　　　　　　　　　　　　 (　　 )

　　 A．288°　 B．144°　 C．72°　　 D．36°

4．用一个半径长为6cm的半圆围成一个圆锥的侧面，则此圆锥的底面半径为　 (　　 ) A．2 cm　 B．3 cm　 C．4 cm　 D．6 cm

5.已知一个扇形的半径为60厘米，圆心角为150°，若用它做成一个圆锥的侧面，则这个圆锥的底面半径为(　　 )

(A)12.5厘米(B)25厘米(C)50厘米(D)75厘米

6.一个圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图扇形的圆心角是(　　 )

(A)60°　 (B)90° (C)120°(D)180°

7.在△ABC中,∠C=90°,BC=a,AC=b(a＞b),分别以AC、BC所在的直线旋转一周,所得的圆锥的侧面积依次是S₁、S₂,则S₁和S₂的大小关系为　　　 (　　 )　　　　　　　　　　　 　

A. S₁＞S₂　　　　 B. S₁＜S₂ C. S₁=S₂　　　 D.以上情况均有可能

8.如图，一个扇形铁皮OAB. 已知OA=60cm，∠AOB=120°，小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝忽略不计)，则烟囱帽的底面圆的半径为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A. 10cm　　　　 B. 20cm　　　 　C. 24cm　　　 　D. 30cm

　

9.如图，圆锥的侧面积恰好等于其底面积的2倍，则该圆锥侧面展开图所对应扇形圆心角的度数为　　　　　　　　　　　　　　　　　　　　 (　　 )

A．　　　 　　 B．　　　　 C．　　　 　 D．

10.若圆锥的母线长为5cm，高为3cm，则其侧面展开图中扇形的圆心角是　　　　 度.

11.已知扇形的圆心角为120°，面积为300πcm² 。(1)扇形的弧长=　　　 ；

(2)若把此扇形卷成一个圆锥，则这个圆锥的轴截面面积是　

12.圆锥的母线为13cm，侧面展开图的面积为65πcm2，则这个圆锥的高为 　　　　　　　　.

13.已知圆锥的底面半径为2,母线长为5,则圆锥的侧面积为　　　　 ,

全面积为　　　　 .

14.若圆锥的锥角为90°,母线长为4,则圆锥的侧面积为　　　　 ,全面积为　　　　 .

15.圆锥的母线长为5cm,高为4cm,它的侧面展开图中,扇形的圆心角为_____度.

16.用一张半圆形纸片围成一个圆锥,则这个圆锥的锥角为　　　　 度.

17.圆锥的轴截面是一个边长为10cm的正三角形,则这个圆锥的高为　　　 cm,

侧面积为　　　　 cm² .

18.如图,在△ABC中,∠C=90°,BC=6,AC=8,以这个直角三角形的一条边所在的直线为轴旋转一周,求所得的几何体的全面积.

19.如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,∠A=60°,BC=2,DC=3, 把直角梯形ABCD以AB所在的直线为轴旋转一周,求所得的几何体的全面积.

　

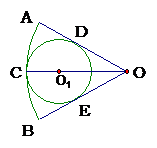
20.如图,在扇形OAB中, ⊙O₁分别与弧AB、OA、OB切于点C、D、E,∠AOB=60°⊙O₁的面积为4,若用此扇形做一个圆锥的侧面,求这个圆锥的高.

　

21.一个圆锥的全面积为340,底面圆的周长为20,求此圆锥侧面展开图的扇形的圆心角.

22、已知圆锥底面半径r=10m，母线长为40m，

(1)求它的侧面展开图的圆心角和表面积；

(2)若一小虫从A点出发沿着圆锥的侧面绕行到母线SA的中点B，求它所走的最短距离。