1．到一个角的两边距离相等的点都在_________.
2．∠AOB的平分线上一点M ，
M到
OA的距离为1.5 cm，则M到OB的距离为_________.
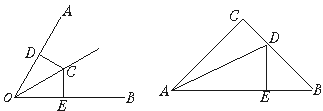
3．如图，∠AOB=60°，CD⊥OA于D，CE⊥OB于E，且CD=CE，则∠DOC=_________.
|
4．如图，在△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，且DE=3 cm，BD=5 cm，则BC=_________ cm．
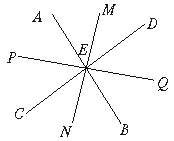
5．如图，已知AB、CD相交于点
E，过E作∠AEC及∠AED的平分线PQ与MN，则直线MN与PQ的关系是_________．
6．三角形内一点到三角形的三边的距离相等，则这个点是三角形_________的交点．
7．
△ABC中，∠C=90°，AD平分∠BAC交BC于D，且BD：CD=3：2，BC=15cm，则点D到AB的距离是__________．
8．角平分线的性质定理：
角平分线上的点_____________________________．
9．(1)如图，已知∠1 =∠2，DE⊥AB，
DF⊥AC，垂足分别为E、F，则DE____DF．
(2)已知DE⊥AB，DF⊥AC，垂足分别
为E、F，且DE = DF，则∠1_____∠2．
10．直角三角形两锐角的平分线所夹的钝角为_______度．
11．
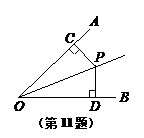如图，OP平分∠AOB，PC
⊥OA，PD⊥OB，垂足分别是C、D．下
列结论中错误的是( )
A．PC = PD B．OC = OD
C．∠CPO = ∠DPO D．OC = PC
12．如图，△ABC中，
∠C
= 90°，AC = BC，AD是∠BAC的平分线，
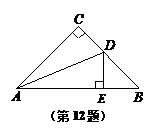DE⊥AB于E，
若AC = 10cm，则△DBE的周长等于( )
A．10cm B．8cm C．6cm
D．9cm
13．到三角形三条边的距离都相等的点是这个三角形的( )
A．三条中线的交点 B．三条高的交点
C．三条边的垂直平分线的交点 D．三条角平分线的交点
14． 如图所示，表示三条相互交叉的公路，现要建一个货物中转站，
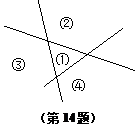要求它到三条公路的距离相等，则可供选择的地址有( )
A．1处 B．2处 C．3处 D．4处
15．给出下列结论，正确的有( )
①到角两边距离相等的点，在这个角的平分线上；②角的平分线与
三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的
逆命题一定是假命题
A．1个 B．2个 C．3个 D．4个
16．已知，Rt△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BC=32，且BD∶CD=9∶7，则D到AB的距离为(
)
A．18 B．16 C．14 D．12
17．
两个三角形有两个角对应相等，正确说法是(
)
A．两个三角形全等
B．两个三角形一定不全等
C．如果还有一角相等，两三角形就全等
D．如果一对等角的
角平分线相等，两三角形全等
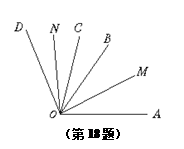
18．如图，OB、OC是∠AOD的任意两条射线，OM平分∠AOB，ON平分∠COD，若∠MON=α，∠BOC=β，则表示∠AOD的代数式为( )
A
．2α－β B．α－β
C．α+β D．2α
19．
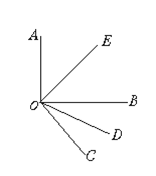(7分)如图，已知OE、OD分别平分∠AOB和∠BOC，若∠AOB
=90°，∠EOD=70°，求∠BOC的度数．
20．(7分)已知：有一块三角形空地，若想在空地中找到一个点，使这个点到三边的距离相等，试找出该点．(保留画图痕迹)
21．(8分)如图，点D、B分别在∠A的两边上，C是∠A
内一点，AB = AD，BC = CD，CE⊥AD于E，CF⊥AF于F．
求证：CE = CF
22．(8分)已知：如图，在△ABC中，∠A=90°，AB = AC，BD平分∠ABC．
求证：BC = AB + AD
23．(8分)如图，PB和PC是△ABC的两条外角平分线．
①求证：∠BPC=90°-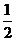
∠BAC．
②根据第①问的结论猜想：三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形？
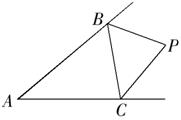
24．(8分)如图，BP是△ABC的外角平分线，点P在∠
BAC的角平分线上．求证：CP是△ABC的外角平分线．
(§11.3)
1．这个角的平分线上 2．1.5cm 3．30° 4．8 5．MN⊥PQ 6．三条角平分线 7．6cm
8．到角的两边的距离相等
9．(1)=(2)= 10．135
11． D 12． B
13．D 14．D 15．B
16．C 17．D 18．A
19．50° 20．画两个角的角平分线的交点P 21．略 22．提示：过点D做DM⊥BC
23．①略；②锐角三角形 24．提示：过P作三边AB、AC、BC的垂线段PD、PE、PF