1.指数函数及其性质
[高考常考角度]
角度1若点在函数的图象上,则的值为( D )
A.
B. C. D.
解析:,,,故选D.
角度2设,则的大小关系是 ( A )
A. B. C.
D.
解析:在时是增函数,所以,在时是减函数,所以。
重点 3 对数函数的图象与性质
[高考常考角度]
角度1函数的单调增区间是__________
解析:由得,由复合函数法则得与的增减性相同,故所求为
角度2已知函数,若,且,则的取值范围是( C )
A. B. C.
D.
点评:本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得,从而错选A,这也是命题者的用苦良心之处.
解析1:因为,所以,所以(舍去),或,所以
又,所以,令,由“对勾”函数的性质知函数在上为减函数,所以,即的取值范围是
解析2:由,且得:,利用线性规划得:,求的取值范围问题,,过点时z最小为3,∴为所求.
角度3设函数,则满足的x的取值范围是( D )
A. B.
C.
D.
解:即解不等式组或;由得;由得,故选择D。
重点 4 幂函数的图象与性质

 高考重点
高考重点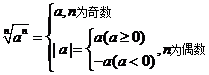 (2)
(2)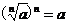 (注意
(注意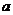 必须使
必须使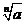 有意义)
有意义)