
网址:http://www.1010jiajiao.com/paper/timu/1658646.html[举报]
23. 如图 ,将三角尺的直角顶点放在直线a上 ,a∥b ,∠1=50°,∠2=60°,
如图 ,将三角尺的直角顶点放在直线a上 ,a∥b ,∠1=50°,∠2=60°,
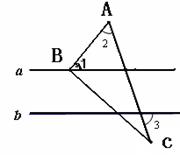 求∠3的度数。(6分)
求∠3的度数。(6分)
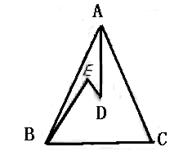 24.如图,在△ABC 中,AB=AC,D、E是△ABC 内两
24.如图,在△ABC 中,AB=AC,D、E是△ABC 内两
点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,
DE=2cm,求BC长。(6分)
2014年八年级数学作业检测卷答案
BCABB DACBD
11. 48 12. 14 13. 10 14. 6 15. 115°
16. 16或17 17.
4 18.
80 19. ①② 20. (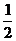 )n-180°
)n-180°
 21. 略
22. 略
21. 略
22. 略
23. .解:∵△BCD中,∠1=50°,∠2=60°,
∴∠4=180°-∠1-∠2=180°-50°-60°=70°,
∴∠5=∠4=70°,
∵a∥b,
 ∴∠3=∠5=70°
∴∠3=∠5=70°
24.延长AD交BC于点G,延长ED交BC于点H,
先证△EBH为等边三角形,可得BH=BE=6,
再由GH=1/2DH=2, 得BG=4
根据三线合一得BC=2BG=8㎝
25. 1)OA=OB=OC (2分)
2)△OMN是等腰三角形 ( 1分)
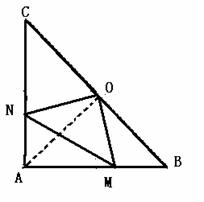 连结OA
连结OA
∵∠BAC=90°,O为BC的中点
∴OA=OB
∵AC=AB , O为BC的中点,∠BAC=90°
∴∠CAO=∠OAB =1/2∠CAB=45°
∠C=∠B=45°
∴∠B=∠CAO,
在△OAN与△OBM中
∵AN=BM, ∠OAN =∠B, OA=OB
∴△OAN≌△OBM (SAS)
∴ON=OM,
∴△OMN是等腰三角形 (3分)
26.解:(1)故答案为:=. (2分)
(2)故答案为:=. (2分)
证明:在等边△ABC中,∠ABC=∠ACB=∠A=60°,
∵EF∥BC,
∴∠AEF=∠ABC=60° ∠AFE=∠ACB=60°,
∴△AEF是等边三角形 ,∠ABC=∠AFE =60°
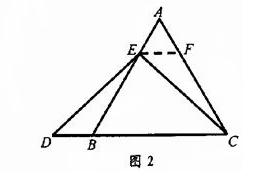 ∴AE=EF,
∴AE=EF,
∵∠ABC=∠AFE =60°,
∴∠EFC=∠EBD,
∵ED=EC,
∴∠D=∠ECB,
∵EF∥BC,
∴∠CEF =∠ECB,
=∠ECB,
∴∠CEF=∠D
在△DBE与△EFC中
∵ ∠EFC=∠EBD,∠CEF=∠D,ED=EC,
∴△DBE≌△EFC,(AAS)
∴DB=EF,
∵EF=EA,
∴AE=BD. (4分)
(3)答:CD的长是1或3. (2分)