
网址:http://www.1010jiajiao.com/paper/timu/2059001.html[举报]
24.如图,在直角坐标系中,点A的坐标为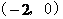 ,点B的坐标为
,点B的坐标为 ,已知抛物线
,已知抛物线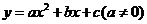 经过三点A、B、O(O为原点).
经过三点A、B、O(O为原点).
(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使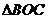 的周长最小.若存在,求出点C的坐标.若不存在,请说明理由;
的周长最小.若存在,求出点C的坐标.若不存在,请说明理由;
(3)如果点P是该抛物线上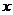 轴上方的一个动点,那么
轴上方的一个动点,那么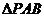 是否有最大面积.若有,求出此时P点的坐标及
是否有最大面积.若有,求出此时P点的坐标及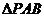 的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号
的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号 ).
).

[答案](1)∵抛物线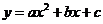 (
(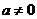 )过点A、B、O,且
)过点A、B、O,且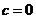 ,
,
解得:
∴所求抛物线的解析式为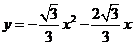 ;
;
(2)存在,由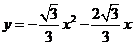 ,配方后得:
,配方后得: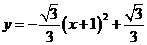 ,
,
抛物线的对称轴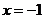 ,
,
∵点C在对称轴上,
△BOC的周长=OB+BC+CO,而OB=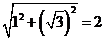 ,
,
要使△BOC的周长周长最小,必须BC+CO最小,
∵点O与点A关于直线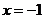 对称,有CO=CA,
对称,有CO=CA,
△BOC的周长=OB+BC+CO= OB+BC+CA.
当A、B、C三点共线时,即点C是直线AB与对称轴的交点时,BC+CA最小,
此时△BOC的周长最小,设直线AB的解析式为: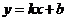 ,则有
,则有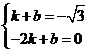 ,
,
解得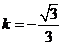 ,
,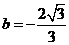 .
.
∴直线AB的解析式为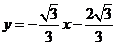 ,
,
当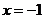 时,
时,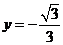 ,
,
∴C的坐标为(-1,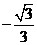 );
);
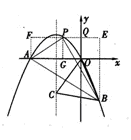
(3)设P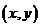 (
(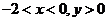 ),
),
则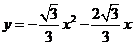 ……………… ①
……………… ①
过点P作PQ⊥ 轴于点Q,PG⊥
轴于点Q,PG⊥ 轴于点G,过点A作AF⊥PQ于点F,过点B作BE⊥PQ于点E,则PQ=
轴于点G,过点A作AF⊥PQ于点F,过点B作BE⊥PQ于点E,则PQ=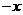 ,PG=
,PG=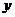 ,
,
由题意得: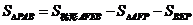 =
=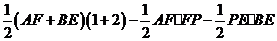
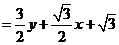
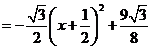 ………………②
………………②
把①代入②得: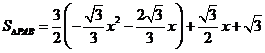
=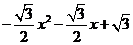
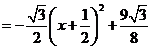 .
.
当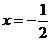 时,△PAB的面积最大,最大值是
时,△PAB的面积最大,最大值是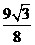 ,
,
此时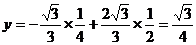 ,
,
∴P的坐标为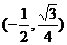 .
.
|
25.如图,在平面直角坐标系 中,矩形 中,矩形 的边 的边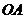 、 、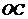 分别在 分别在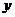 轴和 轴和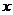 轴的正半轴上,且长分别为 轴的正半轴上,且长分别为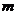 、 、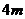  , ,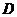 为边 为边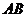 的中点,一抛物线 的中点,一抛物线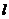 经过点 经过点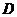 、 、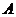 及点 及点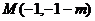 . .(1)求抛物线 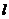 的解析式(用含 的解析式(用含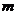 的式子表示); 的式子表示);(2)把 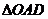 沿直线 沿直线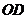 折叠后点 折叠后点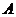 落在点 落在点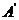 处,连接 处,连接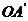 并延长与线段 并延长与线段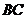 的延长线交于点 的延长线交于点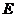 ,若抛物线 ,若抛物线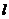 与线段 与线段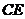 相交,求实数 相交,求实数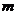 的取值范围; 的取值范围;(3)在满足(2)的条件下,求出抛物线  顶点 顶点 到达最高位置时的坐标. 到达最高位置时的坐标.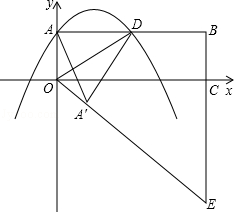 |
|
|
|
|
|
|
 |
 |
||