
网址:http://www.1010jiajiao.com/paper/timu/2219924.html[举报]
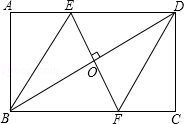
9.(3分)(2014•聊城)如图,在矩形ABCD中,边AB的长为3,点E ,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
|
|
A. |
2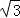 |
B. |
3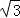 |
C. |
6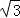 |
D. |
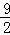 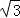 |
|
考点: |
矩形的性质;菱形的性质. |
|
分析: |
根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°,AB=BO=3,因为四边形BEDF是菱形,所以BE,AE可求出进而可求出BC的长. |
|
解答: |
解:∵四边形ABCD是矩形, ∴∠A=90°, 即BA⊥BF, ∵四边形BEDF是菱形, ∴EF⊥BD,∠EBO=∠DBF, ∴AB=BO=3,∠ABE=∠EBO, ∴∠ABE=∠EBD=∠DBC=30°, ∴BE= 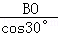 =2 =2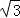 , ,∴BF=BE=2 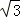 , ,∵EF=AE+FC,AE=CF,EO=FO ∴CF=AE= 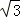 , ,∴BC=BF+CF=3 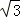 , ,故选B. 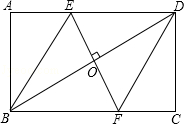 |
|
点评: |
本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半,解题的关键是求出∠ABE=∠EBD=∠DBC=30°. |