
网址:http://www.1010jiajiao.com/paper/timu/2219935.html[举报]
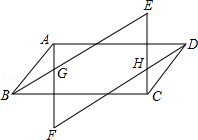
20.(8分)(2014•聊城)如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.
求证:△EBC≌△FDA.
|
考点: |
平行四边形的性质;全等三角形的判定. |
|
专题: |
证明题. |
|
分析: |
根据平行三边的性质可知:AD=BC,由平行四边形的判定方法易证四边形BHDK和四边形AMCN是平行四边形,所以看得∠FAD=∠ECB,∠ADF=∠EBC,进而证明:△EBC≌△FDA. |
|
解答: |
证明:∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC, ∵AF∥CE,BE∥DF, ∴四边形BHDK和四边形AMCN是平行四边形, ∴∠FAD=∠ECB  ,∠ADF=∠EBC, ,∠ADF=∠EBC,在△EBC和△FDA中, 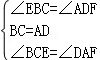 ∴△EBC≌△FDA. 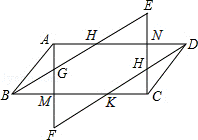 |
|
点评: |
本题考查了平行四边形的判定以及全等三角形的判定,在全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边. |