
网址:http://www.1010jiajiao.com/paper/timu/3824547.html[举报]
16.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=270°.
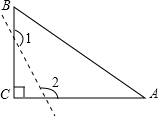
[考点]多边形内角与外角;三角形内角和定理.
[分析]根据四边形内角和为360°可得∠1+∠2+∠A+∠B=360°,再根据直角三角形的性质可得∠A+∠B=90°,进而可得∠1+∠2的和.
[解答]解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
∴∠1+∠2=270°.
故答案为:270°.
[点评]本题是一道根据四边形内角和为360°和直角三角形的性质求解的综合题,有利于锻炼学生综合运用所学知识的能力.