网址：http://www.1010jiajiao.com/paper/timu/3985575.html[举报]
23．如图，抛物线y=x2﹣bx+c与x轴交于A、C两点，与y轴交于B点，已知A点坐标为(1，0)，抛物线的对称轴为直线x=2．
(1)求抛物线的解析式；
(2)求△ABC的面积；
(3)若点P是抛物线对称轴上的一个动点，是否存在点P，使△PAB的周长最小？若存在，求出P点的坐标；若不存在，请说明理由．
[考点]二次函数综合题．
[分析](1)根据A和C关于x=2对称即可求得C的坐标，然后把A和C的坐标代入抛物线解析式求得b和C的值，得到抛物线解析式；
(2)首先求得AC的长，然后利用三角形面价公式求解；
(3)直线BC与对称轴x=2的交点就是P，首先利用待定系数法求得BC的解析式，进而求得P的坐标．
[解答]解：(1)A(1，0)关于x=2的对称点是(3，0)，则C的坐标是(3，0)．
根据题意得：
，
解得：
，
则抛物线的解析式是y=x2﹣4x+3；
(2)AC=3﹣1=2，
则S△ABC=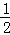
AC•OB=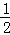×2×3=3；
(3)C是A关于对称轴的对称点，则BC与对称轴的交点就是P．
设BC的解析式是y=kx+d，
则
，
解得：
，
则直线BC的解析式是y=﹣x+3．
当x=2时，y=﹣2+3=1，
则P的坐标是(2，1)．
[点评]本题考查了待定系数法求函数解析式，正确理解P的位置是本题的关键．
