
网址:http://www.1010jiajiao.com/paper/timu/3992760.html[举报]
50、如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.
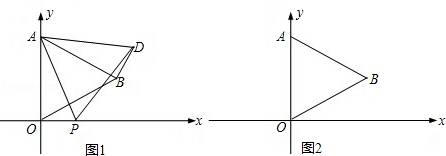
(1)求直线AB的解析式;
(2)当点P运动到点( ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;
(3)是否存在点P,使△OPD的面积等于 ?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
参考答案
1.[解析]
试题分析:连接DO,EO,BE,过点D作DF⊥AB于点F,
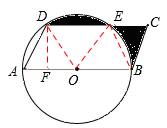
∵AD=OA=1,∴AD=AO=DO。∴△AOD是等边三角形。
∵四边形ABCD是平行四边形,∴DC∥AB。
∴∠CDO=∠DOA=60°,∴△ODE是等边三角形。
同理可得出△OBE是等边三角形且3个等边三角形全等。
∴阴影部分面积等于△BCE面积。
∵DF=ADsin60°=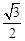 ,DE=EC=1,
,DE=EC=1,
∴图中阴影部分的面积为: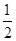 ×
×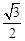 ×1=
×1=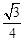 。
。
故选A。
2.[解析]
试题分析:根据特殊角的正切函数值直接作答:tan60°= 。故选C。
。故选C。
3.[解析]
试题分析:
3直接把tan30°=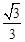 代入进行计算即可:3tan30°=3×
代入进行计算即可:3tan30°=3×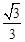 =
= 。故选A。
。故选A。
4.[解析]
试题分析:直接根据特殊角的三角函数值进行解答即可:sin30°=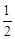 。故选C。
。故选C。
5.A
6.C
7.C
8.C
9.B
10.D
11.[解析]直接由特殊角的三角函数值代入计算即可:
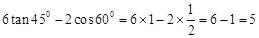 。故选D。
。故选D。
12.[解析]
试题分析:根据题意得:AC=100,∠ABC=30°,
∴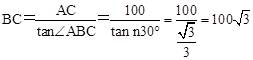 (m)。故选A。
(m)。故选A。
13.[解析]
试题分析:∵∠C=90°,∠A=60°,AC=20m,
∴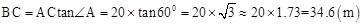 。
。
故选B。
14.[解析]如图,过点P作PH⊥x轴于点H,则
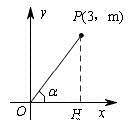
∵P是第一象限内的点,其坐标是(3,m),∴OH=3,PH= m。
又∵OP与x轴正半轴的夹角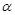 的正切值是
的正切值是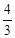 ,即
,即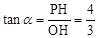 ,
,
∴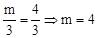 。
。
根据勾股定理,得OP=5。
∴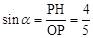 。故选B。
。故选B。
15.[解析]如图,连接AO并延长交圆于点E,连接BE,则∠C=∠E。
由AE为直径,且BD⊥AC,得到∠BDC=∠ABE=90°,
∴△ABE和△BCD都是直角三角形。∴∠CBD=∠EAB。
又∵△OAM是直角三角形, AO=1,
∴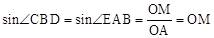 ,即sin∠CBD的值等于OM的长。
,即sin∠CBD的值等于OM的长。
故选A。
16.[解析]∵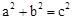 ,∴根据勾股定理逆定理,得△ABC是直角三角形,且∠C=900。
,∴根据勾股定理逆定理,得△ABC是直角三角形,且∠C=900。
∴根据锐角三角函数定义,有:
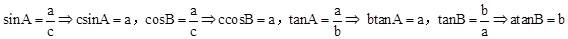 。
。
∴正确的是:csinA= a。故选A。
17.[解析]
试题分析:根据直角三角形全等SAS,HL的判定,使两个直角三角形全等的条件是两条边对应相等。故选D。
18.[解析]
试题分析:如图,连接AE,
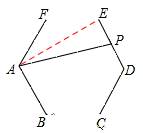
在正六边形中,∠F=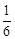 ×(6﹣2)•180°=120°。
×(6﹣2)•180°=120°。
∵AF=EF,∴∠AEF=∠EAF=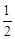 (180°﹣120°)=30°。∴∠AEP=120°﹣30°=90°。
(180°﹣120°)=30°。∴∠AEP=120°﹣30°=90°。
∴AE=2×2cos30°=2×2×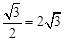 。
。
∵点P是ED的中点,∴EP=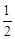 ×2=1。
×2=1。
在Rt△AEP中,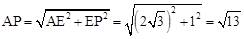 。
。
故选C。
19.[解析]
试题分析:如图,作点C关于OB的对称点C′,交OB于点D,连接AC′交OB于点P,根据轴对称的知识可知,此时A C′=PA+PC最小。
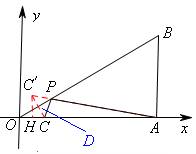
过点C′作 C′H⊥x轴于点H,
∵点B的坐标为(3, ),∴
),∴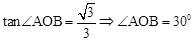 。
。
∵点C的坐标为(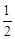 ,0),∴
,0),∴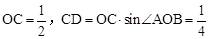 。
。
∴C C′=2CD=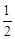 。
。
又∵ ,∴
,∴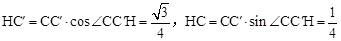 。
。
∴OH=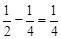 。∴HC=
。∴HC=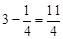 。
。
在Rt△A C′H中,根据勾股定理,得: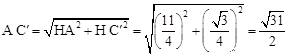 。
。
∴PA+PC的最小值为 。故选B。
。故选B。
20.[解析]∵CD⊥AB,∴△ACD和△BCD都是直角三角形。
∵∠A=450,CD=1,∴AD=CD=1。
∵∠B=300,∴ 。
。
∴AB=AD+BD=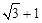 。故选D。
。故选D。
21.[解析](1)结论A正确,理由如下:
解析函数图象可知,BC=10cm,ED=4cm,
故AE=AD﹣ED=BC﹣ED=10﹣4=6cm。
(2)结论B正确,理由如下:
如图,连接EC,过点E作EF⊥BC于点F,
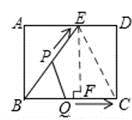
由函数图象可知,BC=BE=10cm,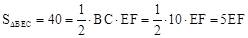 ,
,
∴EF=8。∴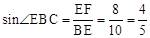 。
。
(3)结论C正确,理由如下:
如图,过点P作PG⊥BQ于点G,
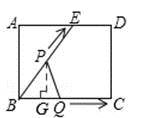
∵BQ=BP=t,∴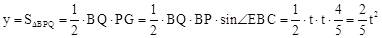 。
。
(4)结论D错误,理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,
设为N,如图,连接NB,NC。
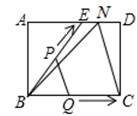
此时AN=8,ND=2,由勾股定理求得:NB=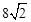 ,NC=
,NC= 。
。
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形。
故选D。
22.[解析]
试题分析:连接AM、AN、过A作AD⊥BC于D,
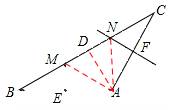
∵在△ABC中,AB=AC,∠A=120°,BC=6cm,
∴∠B=∠C=30°,BD=CD=3cm。∴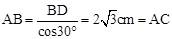 。
。
∵AB的垂直平分线EM,∴BE=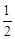 AB=
AB= cm。∴
cm。∴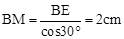 。
。
同理CF= cm,CN=2cm。
cm,CN=2cm。
∴MN=BC﹣BM﹣CN=2cm。故选C。
23.[解析]
试题分析:如图,过A作AD⊥BC于D,则∠BAD=30°,∠CAD=60°,AD=120 m。
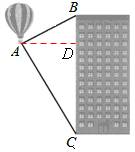
在Rt△ABD中,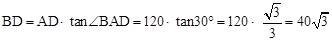 ,
,
在Rt△CD中, ,
,
∴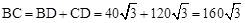 (m)。
(m)。
故选D。
24.D。
25.D
26.[解析]
试题分析:连接AD,则∠ADB=90°,
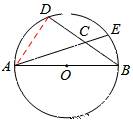
在Rt△ABD中,AB=5,BD=4,则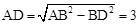 ,
,
∵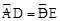 ,∴∠DAC=∠DBA。∴△DAC∽△DBA。
,∴∠DAC=∠DBA。∴△DAC∽△DBA。
∴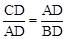 ,即
,即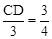 。∴
。∴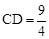 。
。
∴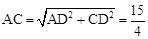 。
。
∴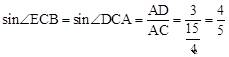 。
。
27.[解析]如图,连接AB、AC、BC,
由题意,点A、B、C为圆上的n等分点,
∴AB=BC,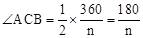 (度)。
(度)。
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BC•cos∠ACB=2cos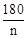 •BC,
•BC,
∴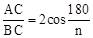 。
。
连接AE、BE,在AE上取一点D,使ED=EC,连接CD,
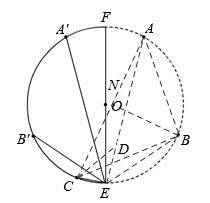
∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形。
∴△ABC∽△CED。∴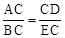 ,∠ACB=∠DCE。
,∠ACB=∠DCE。
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,∴∠ACD=∠BCE。
在△ACD与△BCE中,∵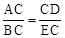 ,∠ACD=∠BCE,∴△ACD∽△BCE。
,∠ACD=∠BCE,∴△ACD∽△BCE。
∴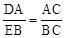 。∴
。∴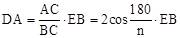 。
。
∴EA=ED+DA=EC+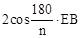 。
。
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC。
∴p=c+ 。
。
当n=4时,p=c+2cos45°•b=c+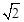 b;
b;
当n=12时,p=c+2cos15°•b=c+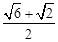 b。
b。
28.[解析]
试题分析:根据特殊角的三角函数值计算即可:sin30°=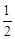 。
。
29.[解析]
试题分析:根据cos30°=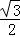 ,继而代入可得出答案.
,继而代入可得出答案.
解:原式=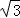 .
.
故答案为: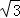 .
.
点评:此题考查了特殊角的三角函数值,属于基础题,解答本题的关键是掌握一些特殊角的三角函数值,需要我们熟练记忆,难度一般.
30.[解析]
分析:将特殊角的三角函数值代入计算即可: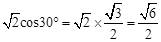 。
。
31.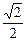
32.0.5
33.4.7
34.[解析]
试题分析:∵在Rt△ABC中,∠ABC=90°,AB=3,BC=4,∴根据勾股定理,得AC=5。
∴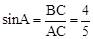 。
。
35.[解析]根据题意,设AB=c,BC=a,AC=b,则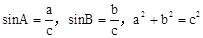 。
。
∵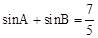 ,
,
∴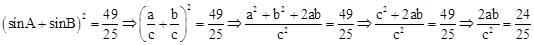 。
。
∴ 。
。
∴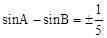 。
。
36.[解析]
试题分析:针对零零指数幂,负整数指数幂,特殊角的三角函数值3个考点分别进行计算,然后根据实数的运算法则求得计算结果:
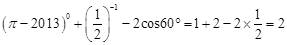 。
。
37.[解析]
试题分析:∵在等边△ABC中,∠B=60°,AB=6,D是BC的中点,∴AD⊥BD,∠BAD=∠CAD=30°。
∴AD=ABcos30°=6×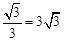 。
。
根据旋转的性质知,∠EAC=∠DAB=30°,AD=AE,
∴∠DAE=∠EAC+∠BAD=60°。∴△ADE的等边三角形。
∴DE=AD=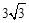 ,即线段DE的长度为
,即线段DE的长度为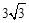 。
。
38.[解析]
试题分析:∵四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°。
∵AE⊥BC,AF⊥CD,∴AB•AE=CD•AF,∠BAE=∠DAF=30°。
∴AE=AF。
∵∠B=60°,∴∠BAD=120°。∴∠EAF=120°﹣30°﹣30°=60°。
∴△AEF是等边三角形。∴AE=EF,∠AEF=60°。
∵AB=4,∴AE=2 。∴EF=AE=2
。∴EF=AE=2 。
。
过A作AM⊥EF,交EF于点M,
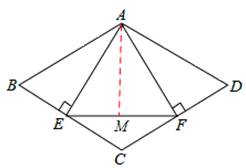
∴AM=AE•cos60°=3。
∴△AEF的面积是: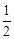 EF•AM=
EF•AM=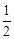 ×2
×2 ×3=3
×3=3 。
。
39.[解析]∵∠DBA=∠DAB=45°,
∴△DAB是等腰直角三角形。
过点D作DE⊥AB于点E,则DE=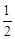 AB,
AB,
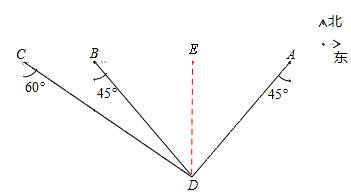
设DE=x,则AB=2x,
在Rt△CDE中,∠DCE=30°,
则CE= DE=
DE= x,
x,
在Rt△BDE中,∠DAE=45°,则DE=BE=x,
由题意得,CB=CE﹣BE= x﹣x=25,
x﹣x=25,
解得:x=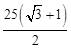 。
。
∴AB=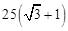 ≈67.5(海里)。
≈67.5(海里)。
40.[解析]
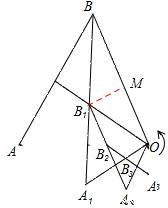
试题分析:∵点B1是面积为1的等边△OBA的两条中线的交点,∴点B1是△OBA的重心,也是内心。
∴∠BOB1=30°。
∵△OB1A1是等边三角形,∴∠A1OB=60°+30°=90°。
∵每构造一次三角形,OBi 边与OB边的夹角增加30°,
∴还需要(360﹣90)÷30=9,即一共1+9=10次构造后等边△OBnAn的边OAn与等边△OBA的边OB第一次重合。
∴构造出的最后一个三角形为等边△OB10A10。
如图,过点B1作B1M⊥OB于点M,
∵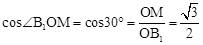 ,
,
∴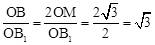 ,即
,即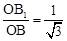 。
。
∴ ,即
,即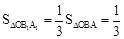 。
。
同理,可得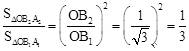 ,即
,即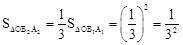 。
。
…,
∴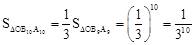 ,即构造出的最后一个三角形的面积是
,即构造出的最后一个三角形的面积是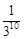 。
。
41.[解析]
试题分析:针对二次根式化简,绝对值,特殊角的三角函数值3个考点分别进行计算,然后根据实数的运算法则求得计算结果。
42.[解析]针对特殊角的三角函数值,绝对值,零指数幂,有理数的乘方,负整数指数幂5个考点分别进行计算,然后根据实数的运算法则求得计算结果。
43.[解析]针对有理数的乘方,特殊角的三角函数值,绝对值,零指数幂4个考点分别进行计算,然后根据实数的运算法则求得计算结果。
44.[解析]针对绝对值,特殊角的三角函数值,有理数的乘方,二次根式化简4个考点分别进行计算,然后根据实数的运算法则求得计算结果。
45.[解析]针对零指数幂,有理数的乘方,绝对值,特殊角的三角函数值,二次根式化简4个考点分别进行计算,然后根据实数的运算法则求得计算结果。
46.[解析]
试题分析:(1)找点A或点B关于CD的对称点,再连接其中一点的对称点和另一点,和MN的交点P就是所求作的位置,根据题意先求出∠C′AE,再根据勾股定理求出AE,即可得出PA+PB的最小值:
如图作点B关于CD的对称点E,连接AE交CD于点P,此时PA+PB最小,且等于A。作直径AC′,连接C′E,
根据垂径定理得弧BD=弧DE。
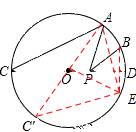
∵∠ACD=30°,∴∠AOD=60°,∠DOE=30°。∴∠AOE=90°。
∴∠C′AE=45°。
又AC为圆的直径,∴∠AEC′=90°。
∴∠C′=∠C′AE=45°。∴C′E=AE=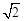 AC′=
AC′=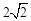 。
。
∴AP+BP的最小值是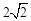 。
。
(2)首先在斜边AC上截取AB′=AB,连接BB′,再过点B′作B′F⊥AB,垂足为F,交AD于E,连接BE,则线段B′F的长即为所求。
47.[解析]
试题分析:(1)过点P作PD⊥AB于点D,构造直角三角形BDP和PDA,PD即为点P到海岸线l的距离,应用锐角三角函数即可求解。
(2)过点B作BF⊥CA于点F,构造直角三角形ABF和BFC,应用锐角三角函数即可求解。
48.[解析]
试题分析:(1)分别在Rt△ADC与Rt△BDC中,利用正切函数,即可求得AD与BD的长,从而求得AB的长。
(2)由从A到B用时2秒,即可求得这辆校车的速度,比较与40千米/小时的大小,即可确定这辆校车是否超速。
49.[解析]
试题分析:(1)如题图2所示,
∵在三角板DEF中,∠FDE=90°,DF=4,DE=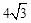 ,
,
∴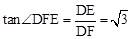 。∴∠DFE=60°。
。∴∠DFE=60°。
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°。
(2)如题图3所示,在Rt△ACF中,解直角三角形即可。
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况,分0≤x≤2,2<x≤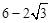 ,
,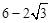 <x≤6三时段讨论:
<x≤6三时段讨论:
当0≤x≤2,即开始到DE与AC重合之前时,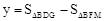 ;
;
当2<x≤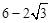 ,即DE与AC重合之后到EF经过点C之前时,
,即DE与AC重合之后到EF经过点C之前时,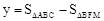 ;
;
当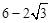 <x≤6,即EF经过点C之后到停止之前时,
<x≤6,即EF经过点C之后到停止之前时,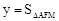 。
。
50.[解析](1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解。
(2)由△ABD由△AOP旋转得到,△ABD≌△AOP,AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形,利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BD•cos60°,DG=BD•sin60°.然后求出OH,DH,然后求出点D的坐标。
(3)分三种情况进行讨论:
①当P在x轴正半轴上时,即t>0时;
②当P在x轴负半轴,但D在x轴上方时;即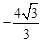 <t≤0时
<t≤0时
③当P在x轴负半轴,D在x轴下方时,即t≤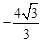 时。
时。
综合上面三种情况即可求出符合条件的t的值。
