(二)新课讲解:
例1.点为所在平面外的一点,点为点在平面内的射影,若,求证:.
证明:连结,
∵,且
∴(三垂线定理逆定理)
同理,∴为的垂心,
∴, 又∵,
∴(三垂线定理)
[练习]:所在平面外的一点在平面内的射影为的垂心,
求证:点在内的射影是的垂心.
例2.已知:四面体中,是锐角三角形,是点在面 上的射影,求证:不可能是的垂心.
证明:假设是的垂心,连结,则,
∵
∴是在平面内的射影,
∴(三垂线定理)
又∵,是在平面内的射影
∴ (三垂线定理的逆定理)
∴是直角三角形,此与“是锐角三角形”矛盾
∴假设不成立,所以,不可能是的垂心.
例3.已知:如图,在正方体中,是的中点,
是的交点,求证:.
证明:,是在面上的射影
又∵,∴
取中点,连结,
∵,
∴为在面上的射影,
又∵正方形中,分别为的中点,∴,
∴(三垂线定理)又∵,∴.

 如图,过直角三角形
如图,过直角三角形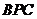 的直角顶点
的直角顶点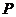 作线段
作线段 平面
平面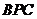 ,
,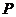 在平面
在平面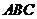 内的射影
内的射影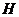 是
是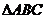 的垂心.
的垂心.