例1.正方体ABCD-A1B1C1D1中.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
∴B1D1∥BD,
又BD Ë平面B1D1C,B1D1平面B1D1C,
∴BD∥平面B1D1C.
同理A1D∥平面B1D1C.
而A1D∩BD=D,
∴平面A1BD∥平面B1CD.
(2)由BD∥B1D1,得BD∥平面EB1D1.取BB1中点G,∴AE∥B1G.
从而得B1E∥AG,同理GF∥AD.∴AG∥DF.
∴B1E∥DF.∴DF∥平面EB1D1.
∴平面EB1D1∥平面FBD.
说明 要证“面面平面”只要证“线面平面”,要证“线面平行”,只要证“线线平面”,故问题最终转化为证线与线的平行.
小结:
例2.如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.
证明:(1) ∵M、N是AB、BC的中点,∴MN∥AC,MN=AC.
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ=CA.
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然ACËα.
否则,若ACÌα,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNÌα,∴AC∥α,
又AC Ëα,∴AC∥α,即AC∥平面MNP.
同理可证BD∥平面MNP.
例3.四面体中,分别为的中点,且,
,求证:平面
证明:取的中点,连结,∵分别为的中点,∴
,又∴,∴在中,
∴,∴,又,即,
∴平面
例2.如图是所在平面外一点,平面,是的中点,是上的点,
(1)求证:;(2)当,时,求的长。
(1)证明:取的中点,连结,∵是的中点,
∴,∵
平面 ,∴ 平面
∴是在平面内的射影
,取 的中点,连结 ,∵∴,又,∴
∴,∴,由三垂线定理得
(2)∵,∴,∴,∵平面.∴,且,∴
课后作业:
1.在长方体中,经过其对角线的平面分别与棱、相交于两点,则四边形的形状为
.(平行四边形)
2.如图,A,B,C,D四点都在平面a,b外,它们在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,在b内的射影A2,B2,C2,D2在一条直线上,求证:ABCD是平行四边形.
证明:∵ A,B,C,D四点在b内的射影A2,B2,C2,D2
在一条直线上,
∴A,B,C,D四点共面.
又A,B,C,D四点在a内的射影A1,B1,C1,D1是平行四边形的四个顶点,
∴平面ABB1A1∥平面CDD1C1.
∴AB,CD是平面ABCD与平面ABB1A1,平面CDD1C1的交线.
∴AB∥CD,同理AD∥BC.∴四边形ABCD是平行四边形.
3.已知直线a、b和平面M、N,且,那么( )
(A)∥Mb⊥a (B)b⊥ab∥M
(C)N⊥Ma∥N (D)
4.如图,矩形所在的平面,分别是的中点,
(1)求证:平面;
(2)求证:
(3)若,求证:平面
5.如图,已知是由一点引出的不共面的三条射线,,求证:
课后记:
课题:直线的倾斜角和斜率(1)
课 型:新授课
教学目标:
知识与技能
1.正确理解直线的倾斜角和斜率的概念.
2.理解直线的倾斜角的唯一性.
3.理解直线的斜率的存在性.
4.斜率公式的推导过程,掌握过两点的直线的斜率公式.
情感态度与价值观
1.通过直线的倾斜角概念的引入学习和直线倾斜角与斜率关系的揭示,培养学生观察、探索能力,运用数学语言表达能力,数学交流与评价能力.
2.通过斜率概念的建立和斜率公式的推导,帮助学生进一步理解数形结合思想,培养学生树立辩证统一的观点,培养学生形成严谨的科学态度和求简的数学精神.
重点与难点: 直线的倾斜角、斜率的概念和公式.
教学方法:启发、引导、讨论.
教学过程:
1.直线的倾斜角的概念
我们知道, 经过两点有且只有(确定)一条直线. 那么, 经过一点P的直线l的位置能确定吗? 如图, 过一点P可以作无数多条直线a,b,c,
…易见,答案是否定的.这些直线有什么联系呢?
(1)它们都经过点P. (2)它们的‘倾斜程度’不同. 怎样描述这种‘倾斜程度’的不同?
引入直线的倾斜角的概念:
当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α= 0°.
问: 倾斜角α的取值范围是什么? 0°≤α<180°.
当直线l与x轴垂直时, α= 90°.因为平面直角坐标系内的每一条直线都有确定的倾斜程度, 引入直线的倾斜角之后, 我们就可以用倾斜角α来表示平面直角坐标系内的每一条直线的倾斜程度.
直线a∥b∥c, 那么它们的倾斜角α相等吗? 答案是肯定的.所以一个倾斜角α不能确定一条直线.
确定平面直角坐标系内的一条直线位置的几何要素:
一个点P和一个倾斜角α.
2.直线的斜率:
一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是
k = tanα
⑴当直线l与x轴平行或重合时, α=0°, k = tan0°=0;
⑵当直线l与x轴垂直时, α= 90°, k 不存在.
由此可知, 一条直线l的倾斜角α一定存在,但是斜率k不一定存在.
例如, α=45°时, k = tan45°=
1;
α=135°时, k = tan135°= tan(180°- 45°) = - tan45°= -
1.
学习了斜率之后, 我们又可以用斜率来表示直线的倾斜程度.
3.直线的斜率公式:
给定两点P1(x1,y1),P2(x2,y2),x1≠x2,如何用两点的坐标来表示直线P1P2的斜率?
可用计算机作动画演示: 直线P1P2的四种情况, 并引导学生如何作辅助线,共同完成斜率公式的推导.(略) 斜率公式:
对于上面的斜率公式要注意下面四点:
(1)
当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角α= 90, 直线与x轴垂直;
(2)k与P1、P2的顺序无关, 即y1,y2和x1,x2在公式中的前后次序可以同时交换, 但分子与分母不能交换;
(3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得;
(4)
当 y1=y2时, 斜率k = 0, 直线的倾斜角α=0°,直线与x轴平行或重合.
(5)求直线的倾斜角可以由直线上两点的坐标先求斜率而得到.
4.例题:
例1 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断它们的倾斜角是钝角还是锐角.
略解: 直线AB的斜率k1=1/7>0, 所以它的倾斜角α是锐角;
直线BC的斜率k2=-0.5<0, 所以它的倾斜角α是钝角;
直线CA的斜率k3=1>0, 所以它的倾斜角α是锐角.
例2 在平面直角坐标系中, 画出经过原点且斜率分别为1, -1, 2, 及-3的直线a,
b, c, l.
分析:要画出经过原点的直线a, 只要再找出a上的另外一点M. 而M的坐标可以根据直线a的斜率确定; 或者k=tanα=1是特殊值,所以也可以以原点为角的顶点,x
轴的正半轴为角的一边, 在x 轴的上方作
45°的角, 再把所作的这一边反向延长成直线即可.
略解: 设直线a上的另外一点M的坐标为(x,y),根据斜率公式有
1=(y-0)/(x-0),所以 x = y
可令x = 1, 则y = 1, 于是点M的坐标为(1,1).此时过原点和点M(1,1),
可作直线a.同理, 可作直线b, c, l.(用计算机作动画演示画直线过程)
5.练习: P86
1. 2. 3. 4.
课堂小结:
(1)直线的倾斜角和斜率的概念.
(2) 直线的斜率公式.
课后作业: P89 习题3.1 1.
2. 3.4
课后记:
课题:直线的倾斜角和斜率(2)
课 型:习题课
教学目标:
1.进一步加深理解直线的倾斜角和斜率的定义
2.已知直线的倾斜角,会求直线的斜率
3.已知直线的斜率,会求直线的倾斜角
4.培养学生分析探究和解决问题的能力.
教学重点:直线的倾斜角和斜率的应用
教学难点:斜率概念理解与斜率公式的灵活运用
教学过程
1.复习:1)说出倾斜角和斜率的概念,它们都反映了直线的什么牲特征?
2)
斜率的计算公式是什么?
2.巩固练习:
1)已知直线的倾斜角,口答直线的斜率:
(1) =0°;(2)=60°;(3) =90°;(4)150°
2).直线经过原点和点(-1,-1),则它的倾斜角是
3).过点P(-2,m)和Q(m,4)的直线的斜率等于1,则m的值为(
)
A.1
B.4 C.1或3
D.1或4
4).已知A(2,3)、B(-1,4),则直线AB的斜率是 .
5).已知M(a,b)、N(a,c)(b≠c),则直线MN的倾斜角是
.
6).已知O(0,0)、P(a,b)(a≠0),直线OP的斜率是
.
7).已知,当时,直线的斜率 =
;当且时,直线的斜率为
3.例题分析:
例1.若三点,,共线,求的值
解:
说明:本题旨在让学生了解斜率也可研究直线的位置关系,为下节课的学习打基础
例2.如果直线经过A(-1,2m)、B(2,)二点,求直线的斜率K的取值范围。
例3.若直线的斜率为函数
例4.已知两点A(-3,4)、B(3,2),过点P(2,-1)的直线与线段AB有公共点.求直线的斜率k的取值范围.( k≤-1或k≥3)
4.提高练习
1.若直线过(-2,3)和(6,-5)两点,则直线的斜率为
,倾斜角为
2.已知直线l1的倾斜角为1,则l1关于x轴对称的直线l2的倾斜角2为________.
3已知两点A(x,-2),B(3,0),并且直线AB的斜率为,则x=
4斜率为2的直线经过(3,5)、(a,7)、(-1,b)三点,则a、b的值是(
)
A.a=4,b=0 B.a=-4,b=-3
C.a=4,b=-3 D.a=-4,b=3
5已知两点M(2,-3)、N(-3,-2),直线l过点P(1,1)且与线段MN相交,则直线的斜率k的取值范围是( )
A.k≥或k≤-4 B.-4≤k≤
C. ≤k≤4 D.-≤k≤4
归纳小结:解题时,要重视数学思想方法的应用.
作业布置:完成全优设置相关练习.
课后记:
课题:两条直线的平行与垂直
课 型:新授课
教学目标:理解并掌握两条直线平行与垂直的条件,会运用条件判定两直线是否平行或垂直.
教学重点:两条直线平行和垂直的条件是重点,要求学生能熟练掌握,并灵活运用.
教学难点:启发学生, 把研究两条直线的平行或垂直问题, 转化为研究两条直线的斜率的关系问题.
注意:对于两条直线中有一条直线斜率不存在的情况, 在课堂上老师应提醒学生注意解决好这个问题.
教学过程:

 的直线都可以写成
的直线都可以写成 ;
; 的直线都可以用
的直线都可以用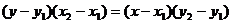 表示;
表示;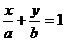 表示;
表示; 的直线都可以用
的直线都可以用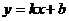 表示;
表示;