网址：http://www.1010jiajiao.com/paper/timu/4037594.html[举报]

(三)、知识应用与解题研究：

例1．判断下列二元二次方程是否表示圆的方程？如果是，请求出圆的圆心及半径。

学生自己分析探求解决途径：①、用配方法将其变形化成圆的标准形式。②、运用圆的一般方程的判断方法求解。但是，要注意对于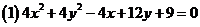来说，这里的

.

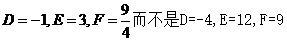解：

例2．(课本例4)求过三点A(0，0)，B(1，1)，C(4，2)的圆的方程，并求这个圆的半径长和圆心坐标。

　 分析：据已知条件，很难直接写出圆的标准方程，而圆的一般方程则需确定三个系数，而条件恰给出三点坐标，不妨试着先设出圆的一般方程　

解：设所求的圆的方程为：

∵在圆上，所以它们的坐标是方程的解.把它们的坐标代入上面的方程，可以得到关于的三元一次方程组.

即

解此方程组，可得：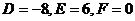

∴所求圆的方程为：

；

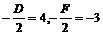
得圆心坐标为(4，-3).

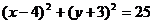或将左边配方化为圆的标准方程，,从而求出圆的半径，圆心坐标为(4,-3)

学生讨论交流，归纳得出使用待定系数法的一般步骤：

①、根据提设，选择标准方程或一般方程；

②、根据条件列出关于a、b、r或D、E、F的方程组；

③、解出a、b、r或D、E、F，代入标准方程或一般方程。

例3、已知线段AB的端点B的坐标是(4，3)，端点A在圆上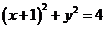

运动，求线段AB的中点M的轨迹方程。

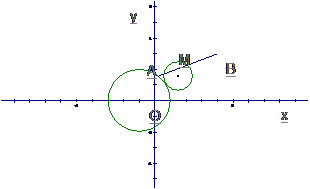
分析：如图点A运动引起点M运动，而点A在已知圆上运动，点A的坐标满

足方程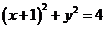。建立点M与点A坐标之间的关系，就可以建立点M的坐标满足的条件，求出点M的轨迹方程。　　　　　　　　　　　　　　　　　　　

解：设点M的坐标是(x,y),点A的坐标是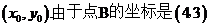

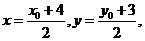
　 　① 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

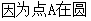
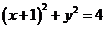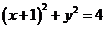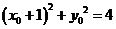
上运动，所以点A的坐标满足方程,即②

把①代入②，得

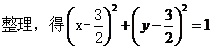
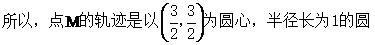
课堂练习： 第1、2、3题

课堂小结 ：

1．对方程的讨论(什么时候可以表示圆)

2．与标准方程的互化

3．用待定系数法求圆的方程

4．求与圆有关的点的轨迹。

课后作业：课本习题4.1A组第6题,B组第1,2题

课后记:

课题：直线与圆的位置关系(第一课时)

课　　 型：新授课

教学目标：1、理解直线与圆的位置的种类；

2、利用平面直角坐标系中点到直线的距离公式求圆心到直线的距离；

3、会用点到直线的距离来判断直线与圆的位置关系．

教学重点：直线与圆的位置关系的几何图形及其判断方法

教学难点：用坐标法判断直线与圆的位置关系．

教学过程：