
网址:http://www.1010jiajiao.com/paper/timu/5140304.html[举报]
18、某珍稀植物种子在一定条件下发芽成功的概率为 ,该研究性学习小组又分成两个
,该研究性学习小组又分成两个
小组进行验证性实验.
(Ⅰ)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(Ⅱ)第二小组做了若干次发芽实验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数 的概率分布列和平均试验的次数.
的概率分布列和平均试验的次数.
周练(18)参考答案及部分解答
一、选择题(每小题5分,共60分):
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
D |
B |
D |
B |
B |
C |
D |
A |
D |
D |
C |
B |
二、填空题(每小题4分,共16分)
13. 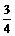 14.
14.
15、 16、
16、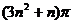 .
.
三、解答题(共74分,按步骤得分)
17.解:由条件, ,
,
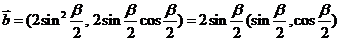 ,
,
∵ ,∴
,∴ .
.
故 ,
, ……4分
……4分
 ,∴
,∴
 ……8分
……8分
∵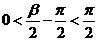 ,∴
,∴ ,
,
又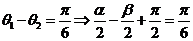 ,∴
,∴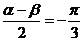 , ……10分
, ……10分
故 ……12分
……12分
18.解:(1)至少有3次发芽成功,即有3次、4次、5次发芽成功
∴所求概率 -------------------------------------------4分
-------------------------------------------4分
(2)ξ的分布列为
|
---------------------------------------------8分

19、解:(1)∵ ,且曲线在
,且曲线在 时取极值,
时取极值,
∴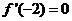 ,即有
,即有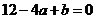 . ①
……2分
. ①
……2分
∵切点P(1,0),∴P在曲线上,得
 ,∴
,∴ . ②
……3分
. ②
……3分
并且在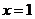 处,切线斜率为
处,切线斜率为 ,∴
,∴ ,∴
,∴ ,
,
即: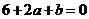 .
③
……4分
.
③
……4分
由①②③解得: ,∴
,∴ .……6分
.……6分
(II)∵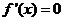 ,得
,得 ,
……7分
,
……7分
当 或
或 时,
时,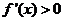 ,当
,当 时,
时, ,
,
故函数在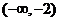 及
及 内单调递增,在
内单调递增,在 内单调递减. ……9分
内单调递减. ……9分
又∵ ,
, ,
, ,
, , ……10分
, ……10分
∴
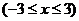 ,当
,当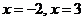 时,
时, ,
,
当 时,
时, . ……12分
. ……12分
20.(1)证明:∵  是菱形,∠
是菱形,∠ =60°
=60° △
△ 是正三角形
是正三角形
又∵ 
 5分
5分
(2) ∴ ∠BEM为所求二面角的平面角
∴ ∠BEM为所求二面角的平面角
△ 中,
中, 60°
60° ,Rt△
,Rt△ 中,
中,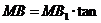 60°
60°
∴  , ∴ 所求二面角的正切值是2; 10分
, ∴ 所求二面角的正切值是2; 10分
(3) .14分
.14分
21、解析:(Ⅰ) 设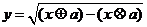 ,
,
则 , 又由
, 又由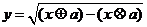 ≥0 ,
≥0 ,
可得P( ,
, ) 的轨迹为
) 的轨迹为 ;
--------- 4 分
;
--------- 4 分
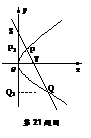
(Ⅱ) 由已知可得 , 整理得
, 整理得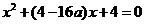 ,
,
由 ,得
,得 .
.
∵ ,∴
,∴ .∴
.∴
 ,解得
,解得 .
------- 8 分
.
------- 8 分
(Ⅲ) ∵ ,∴
,∴
设直线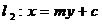 , 依题意
, 依题意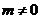 ,
,  ,则
,则
分别过P、Q作PP1⊥ y轴,QQ1⊥ y轴,垂足分别为P1、Q1,则

 .
.
由 消去y ,得
消去y ,得 .
.
∴ ≥
≥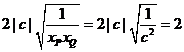 .
.
∵ 、
、 可取一切不相等的正数,
可取一切不相等的正数,
∴ 的取值范围是(2,+
的取值范围是(2,+ ).
--------- 12分
).
--------- 12分
22.解:(I)设动点P(x,y),由题意|x| |y|=1,因为P在第一象限,
|y|=1,因为P在第一象限,
∴曲线C的方程为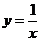 .
……1分.
.
……1分.
由题意直线OB1,A1B2,…,AnBn+1的斜率都是1. ……2分
∵直线OB1方程为 ,由
,由 ,得
,得 ,∴
,∴ …4分
…4分
类似直线AnBn+1的方程为 ,由
,由 ,得
,得
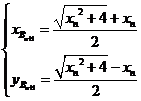 ,∴
,∴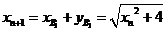 , ……6分
, ……6分
∴ ,从而
,从而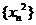 是以4为首项,4为公差的等差数列, ……7分
是以4为首项,4为公差的等差数列, ……7分
∴ ,故
,故 .
……8分
.
……8分
(II)∵ ,
……10分
,
……10分
∴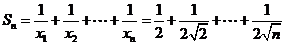
 ……12分
……12分
∴当 时,
时, ;
;
当 时,
时, . ……14分
. ……14分