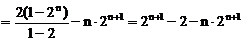网址:http://www.1010jiajiao.com/paper/timu/5142107.html[举报]
4.从原点向圆 x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为
A.π B.2π C.4π D.6π
范水高级中学2005~2006年度第一学期高三数测试题数学试卷答案
一、选择题
1. B 2. A 3. C 4. B 5. D 6. C
7. C 8. A 9. B 10. D 11. A 12. A
二、填空题
13. 216 14.[-6,2] 15.
1 16. 155 17.  18.
18. 
三、解答题
19. 解:由于 在R上是增函数,所以,
在R上是增函数,所以, 等价于
等价于
 ①………………………………………(2分)
①………………………………………(2分)
(1)当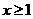 时,
时, ,所以①式恒成立. …………………(4分)
,所以①式恒成立. …………………(4分)
(2)当 时,
时,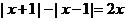 ,①式化为
,①式化为 ,即
,即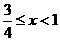 .…(8分)
.…(8分)
(2)当 时,
时, ,①式无解,……………………(10分)
,①式无解,……………………(10分)
综上, 的取值范围是
的取值范围是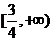 .…………………………………………(12分)
.…………………………………………(12分)
20. 解:(1)由题意知,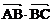

 , ………………①
, ………………①

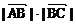
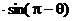

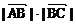
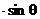 ,…………②………(2分)
,…………②………(2分)
由②÷①, 得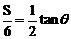 , 即
, 即
由 得
得 , 即
, 即 .……………(4分)
.……………(4分)
又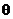 为
为 与
与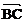 的夹角, ∴
的夹角, ∴ , ∴
, ∴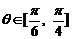 .……………(6分)
.……………(6分)
(2)
 ……………(9分)
……………(9分)
∵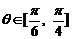 , ∴
, ∴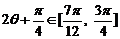 .……………(10分)
.……………(10分)
∴ , 即
, 即 时,
时,  的最小值为3. ……………(12分)
的最小值为3. ……………(12分)
21. 解:(1)依题意,第二年该商品年销售量为(11.8-p)万件,年销售收入为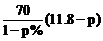 万元,
万元,
则商场该年对该商品征收的总管理费为 万元,……(2分)
万元,……(2分)
故所求函数为 .…………(4分)
.…………(4分)
由11.8-p>0及p>0得定义域为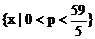 .…………(6分)
.…………(6分)
(2)由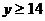 得
得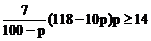 .…………(8分)
.…………(8分)
化简得 ,即
,即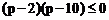 ,解得
,解得 .………(9分)
.………(9分)
故当比率在[2%,10%]内时,商场收取的管理费将不少于14万元. …………(10分)
(3)第二年,当商场的管理费不少于14万元时,厂家的销售收入为
 ,…………(12分)
,…………(12分)
因为 在区间
在区间 上为减函数,
上为减函数,
所以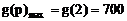 万元. …………(13分)
万元. …………(13分)
故当比率为2%时,厂家销售额最大,且商场收管理费又不少于14万元. ………(14分)
22. 解:(I)证明:在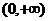 上任取两数
上任取两数 ,且
,且 ,
,
则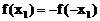 ,
,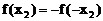 且
且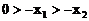 ,…………(2分)
,…………(2分)
∵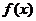 在
在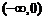 上是增函数,∴
上是增函数,∴ 即
即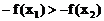 ,
,
∴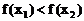 .
.
即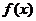 在区间
在区间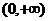 上是增函数. …………(4分)
上是增函数. …………(4分)
(II) ∵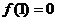 ,∴
,∴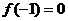 …………(6分)
…………(6分)
当 时,有
时,有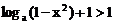 ,∴
,∴ ,…(8分)
,…(8分)
①
当 时,
时,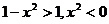 ,无解,…………(9分)
,无解,…………(9分)
当 时,
时,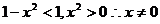 .…………(10分)
.…………(10分)
②
当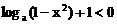 时,有
时,有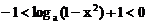 ,
,
即 .
.
当 时,
时,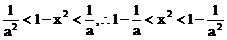 ,
,
∴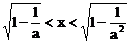 或
或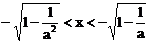 ;…………(12分)
;…………(12分)
当 时,
时,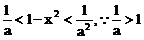 而
而 …………(13分)
…………(13分)
综上所述,当 时,原不等式的解集为
时,原不等式的解集为 且
且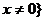
当 时,原不等式的解集为
时,原不等式的解集为
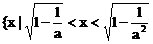 或
或 ………(14分)
………(14分)
23. 解:(I)由 令
令

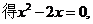 解得
解得
即f(x)存在两个滞点0和2 
(II)由题得 ,
, ①
①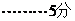
故 ②
②
由②-①得 ,
,
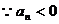
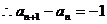 ,即
,即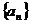 是等差数列,且
是等差数列,且

当n=1时,由


(III) ③
③
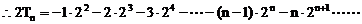 ④
④
由④-③得