
网址:http://www.1010jiajiao.com/paper/timu/5142457.html[举报]
5.如图,在Rt△ABC中,∠C=90°,DE⊥AB,AC=BE=15,BC=20。则四边形ACED的面积为( )
(A) 54 (B) 75 (C) 90 (D) 96

参考答案:
一、选择题:
1、B;2、C ;3、A;4、A;5、D;6、A;7、B;8、C;9、C;10、B。
二、填空题:
11、3;12、60°;13、7.5;14、(3,4);15、30°;16、 ;17、2;18、7.5_;19、19;20、20;21、22;22、4。
;17、2;18、7.5_;19、19;20、20;21、22;22、4。
三、解答题:
23、解:(1)设A(x,0)、B(x+3,0)、C(0,y),
根据切割线定理,
 。
。
解得:x=1或x=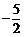 (舍)。∴y=-2。
(舍)。∴y=-2。
∴A、B、C三点的坐标分别是A(1,0)、B(4,0)、C(0,-2)。
(2)设过两点的抛物线为y=a(x-1)(x-4),
∵它过点C(0,-2),∴-2=a(0-1)(0-4),∴a=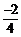 =
=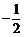 。
。
∴抛物线的方程为y=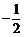 (x-1)(x-4)。
(x-1)(x-4)。
24、解:(1)一个平方数的末位数字(非0)只能是1,4,5,6,9。
∴数n的末二位必然是11,44,55,66,99,
又n为平方数,∴n≡0或1(mod 4)。
而末二位是11,55,99的数同余于3(mod 4),末二位是66的数同余于2(mod 4)。
∴a只能为4,如144=122。
(2)若至少有连续4个4,即n=m2=t.104+4444。
∴可设m=2m1,m12=25t.102+1111≡3(mod 4)。
同(1)可知,25t.102+1111不能为完全平方数。
∴至多连续3个4。(能够做到,见(3))
(3)当k最大时,最小的具有这样性质的数为1444=382。
25、证明:
 △BEC∽△DCF,
△BEC∽△DCF,
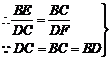 ∴
∴ 。
。
∴△BED∽△DBF,
∴∠BED=∠DBM。
∴∠BME=∠BDM+∠DBM
=∠BDM+∠BED=∠ABD=60°。
∴由正弦定理得:2R1=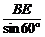 ,2R2=
,2R2=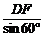 ,
,
∴R1.R2=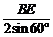 .
. =
=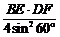 =
=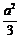 。
。