
网址:http://www.1010jiajiao.com/paper/timu/5142503.html[举报]
6.下列四个函数:①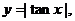 ②
②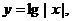 ③
③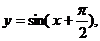 ④
④ 其中是偶函数,
其中是偶函数,
又在区间(-1,1)内连续的函数的个数是 ( )
A.0 B.1 C.2 D.3
2004年三月高三第二次联考
数学(理科)参考答案及评分细则
一、AACBC CBBCD DB
二、13.(2,1,-3,-2)(只要写出的一组值适合条件即可)
14.36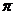 15.
15. 16.
16.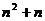
三、17.解:依题意有(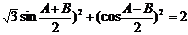 ……3′
……3′
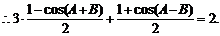 ……6′
……6′
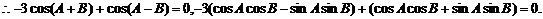
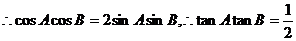 ……12′
……12′
18.解法1:(1)延长B1E交BC于F,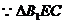 ∽△FEB,BE=
∽△FEB,BE=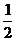 EC1
EC1
∴BF=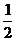 B1C1=
B1C1=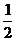 BC,从而F为BC的中点.……2′
BC,从而F为BC的中点.……2′
∵G为△ABC的重心,∴A、G、F三点共线.
且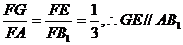 ,又GE
,又GE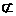 侧面AA1B1B,∴GE//侧面AA1B1B……6′
侧面AA1B1B,∴GE//侧面AA1B1B……6′
(2)在侧面AA1B1B内,过B1作B1H⊥AB,垂足为H,∵侧面AA1B1B⊥底面ABC,
∴B1H⊥底面ABC. 又侧棱AA1与底面ABC成60°的角,AA1=2,
∴∠B1BH=60°,BH=1,B1H=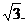 在底面ABC内,过H作HT⊥AF,垂足为T,
在底面ABC内,过H作HT⊥AF,垂足为T,
连B1T. 由三垂线定理有B1T⊥AF,又平面B1CE与底面ABC的交线为AF,
∴∠B1TH为所求二面角的平面角.……9′
∴AH=AB+BH=3,∠HAT=30°,∴HT=AH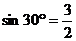 ,
,
在Rt△B1HT中,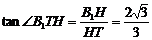 ,从而平面B1GE与底面ABC成锐二面角的大小为
,从而平面B1GE与底面ABC成锐二面角的大小为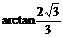 ……12′
……12′
解法2:
(1)∵侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,∴∠A1AB=60°,
又AA1=AB=2,取AB的中点O,则AO⊥底面ABC. 以O为原点建立空间直角坐标系
O-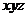 如图. 则A(0,-1,0),B(0,1,0),C(
如图. 则A(0,-1,0),B(0,1,0),C(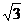 ,0,0),A1(0,0,
,0,0),A1(0,0,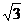 ),
),
B1(0,2,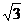 ),C1(
),C1(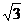 ,1,
,1,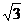 ). ……3 ′
). ……3 ′
∵G为△ABC的重心,∴G(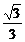 ,0,0),
,0,0),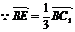
∴E(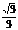 ,1,
,1,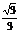 ) ∴
) ∴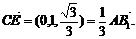
又GE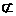 侧面AA1B1B,∴GE//侧面AA1B1B……6′
侧面AA1B1B,∴GE//侧面AA1B1B……6′
(2)设平面B1GE的法向量为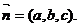 则由
则由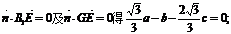
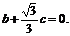 可取
可取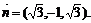 ……8′ 又底面ABC的法向量为
……8′ 又底面ABC的法向量为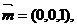 …9′
…9′
设平面B1GE与底面ABC所成锐二面角的大小为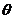 ,
,
则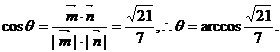 ……12′
……12′
19.解:(1)当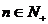 时有:
时有: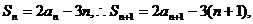
两式相减得: ……3′
……3′
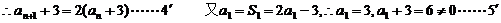
∴数列{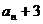 }是首项6,公比为2的等比数列.
}是首项6,公比为2的等比数列.
从而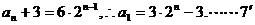 另解:归纳猜想再用数学归纳法证,过
另解:归纳猜想再用数学归纳法证,过
程略,请相应给分.
(2)假设数列{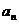 }中存在三项
}中存在三项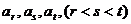 ,它们可以构成等差数列,
,它们可以构成等差数列,
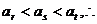 只能是
只能是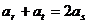 ,
,
即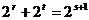 ……9′
……9′  、
、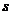 、
、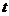 均为正整数,
均为正整数,
∴(*)式左边为奇数右边为偶数,不可能成立. 因此数列{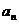 }中不存在可以构成等差
}中不存在可以构成等差
数列的三项.……12′
20.解:(1)记路段MN发生堵车事件为MN.
因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所
以路线A→C→D→B中遇到堵车的概率P1为
1-P(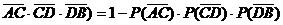
=1-[1-P(AC)][1-P(CD)][1-P(DB)]
=1-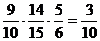 ;……2′
;……2′
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(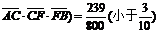 …3′路线A→E→F→B中遇到堵车的概率P3为1-P(
…3′路线A→E→F→B中遇到堵车的概率P3为1-P( ……4′
……4′
显然要使得由A到B的路线途中发生堵车事件的概率最小.只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小.……6′
(2)路线A→C→F→B中遇到堵车次数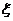 可取值为0,1,2,3.
可取值为0,1,2,3.
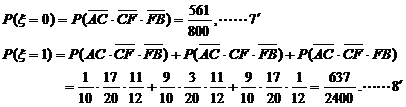
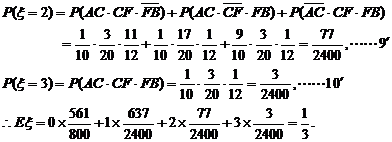
答:路线A→C→F→B中遇到堵车次数的数学期望为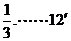
21.解(1)(方法1)在双曲线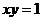 上任取不同三点
上任取不同三点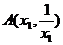 、
、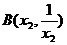 、
、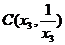 设
设
△ABC的垂心H为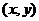 .由
.由 ,
,
及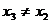 得:
得: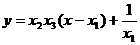 …………①………………2′
…………①………………2′
同理由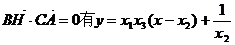 …………②…………3′
…………②…………3′
由①、②解得: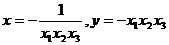 .
.
H点的坐标适合方程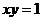 ,
,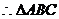 的垂心H也该双曲线上.…………5′
的垂心H也该双曲线上.…………5′
(方法2)求出两条高线方程,解出H坐标,仿上给分.
(2)设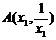 、
、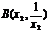 ,
,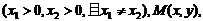
由已知有: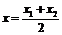 ;……③
;……③ 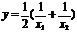 ;……④
;……④
 ……⑤……8′
由③④得:
……⑤……8′
由③④得: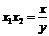 ……⑥
……⑥
由③⑥代入⑤整理得: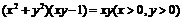 为所求点M的轨迹方程…10′
为所求点M的轨迹方程…10′
(3)由(2)知: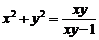 ;……⑦
;……⑦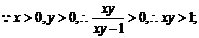 ……12′
……12′
又 (当且仅当
(当且仅当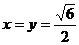 时取等号)
时取等号)
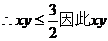 的取值范围是
的取值范围是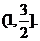 ……14′
……14′
22.解:(1)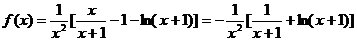 ……3′
……3′
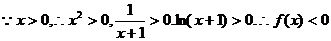 .
.
因此函数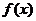 在区间(0,+∞)上是减函数.……5′
在区间(0,+∞)上是减函数.……5′
(2)(方法1)当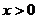 时,
时,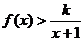 恒成立,令
恒成立,令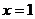 有
有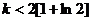
又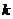 为正整数.
为正整数. 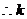 的最大值不大于3.……7′
的最大值不大于3.……7′
下面证明当
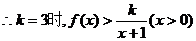 恒成立.
恒成立.
即证当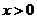 时,
时,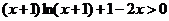 恒成立.……9′
恒成立.……9′
令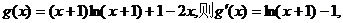
当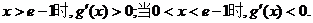
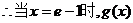 取得最小值
取得最小值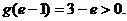
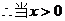 时,
时,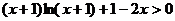 恒成立.
恒成立.
因此正整数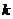 的最大值为3.……12′
的最大值为3.……12′
(2)(方法2)当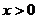 时,
时,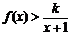 恒成立,
恒成立,
即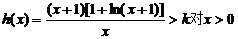 恒成立.
恒成立.
即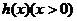 的最小值大于
的最小值大于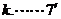
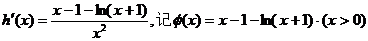
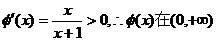 上连续递增,
上连续递增,
又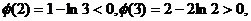
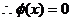 存在唯一实根
存在唯一实根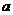 ,且满足:
,且满足: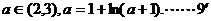
由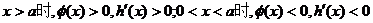 知:
知:
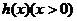 的最小值为
的最小值为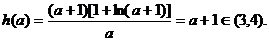
因此正整数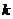 的最大值为3.……12′
的最大值为3.……12′