
网址:http://www.1010jiajiao.com/paper/timu/5142650.html[举报]
6. 已知直线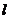 、m,平面
、m,平面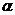 、β,且
、β,且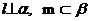 给出下列命题
①若
给出下列命题
①若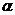 ∥β,则
∥β,则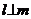 ②若
②若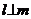 ,则
,则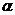 ∥β ③若
∥β ③若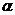 ⊥β,则
⊥β,则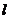 //m ④若
//m ④若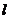 ∥m,则
∥m,则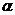 ⊥β,其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
⊥β,其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
参考答案
一、选择题
|
题 号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答 案 |
D |
C |
A |
D |
D |
B |
A |
B |
C |
D |
A |
C |
二、填空题
13. {x|x≤―2或x=1} 14. 7 15. 18 16. 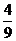
三、解答题(共74分)
17.(1)∵这名学生在第一、二个路口没遇到红灯,第三个路口遇到红灯。
∴概率P=(1―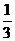 )(1―
)(1―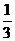 )×
)×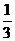 =
=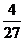
(2)(理)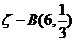 ∴
∴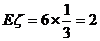
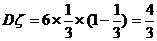 (文)
(文)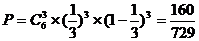
18.∵α∈(0,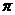 ),β∈(
),β∈(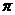 ,2
,2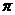 ), ∴
), ∴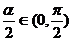 ,
,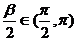
又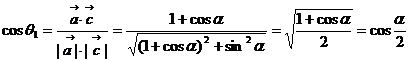 ,
,
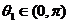 ∴
∴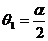
又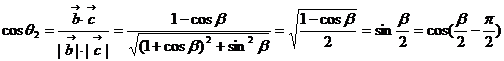
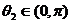 且
且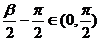 ,
,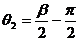
∴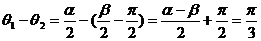 ∴
∴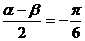
∴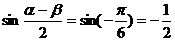
19.解(1)令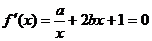 则2bx2+x+a=0
则2bx2+x+a=0
由题意知:x=1,2是上方程两根,由韦达定理:
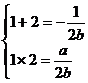 ∴
∴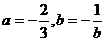 (2)由(1)知:
(2)由(1)知: 令
令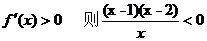 解得:x<0或1<x<2
∴f(x)的单调增区间为(1,2) 减区间是(0,1)和(2,+
解得:x<0或1<x<2
∴f(x)的单调增区间为(1,2) 减区间是(0,1)和(2,+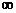 )
(3)由(2)知:f(x)在x1=1处取极小值,在x2=2处取极大值。
20.(1)以A为原点,AB、AD、AA1所在直线为x轴,y轴,z轴。
)
(3)由(2)知:f(x)在x1=1处取极小值,在x2=2处取极大值。
20.(1)以A为原点,AB、AD、AA1所在直线为x轴,y轴,z轴。
则D(0,8,0),A1(0,0,4),M(5,2,4)
 ∴
∴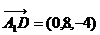
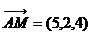
∵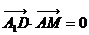 ∴
∴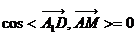
(2)由(1)知A1D⊥AM,又由已知A1D⊥AN, ∴A1D⊥平面AMN,垂足为N。
因此AD与平面所成的角即是∠DAN。
易知∠DAN = AA1D = arctan2
(3)∵AA1⊥平面ABCD,A1N⊥平面AMN,
∴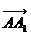 和
和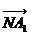 分别成为平面ABCD和平面AMN的法向量。
设平面AMN与平面ABCD所成的角(锐角)为
分别成为平面ABCD和平面AMN的法向量。
设平面AMN与平面ABCD所成的角(锐角)为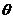 ,则
,则
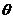 =(
=(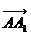 ,
,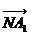 )=∠AA1N = AA1D = arccos
)=∠AA1N = AA1D = arccos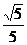
21.(1)解:设P(a,0),Q(0,b)
则: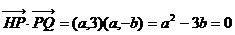 ∴
∴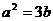
设M(x,y)∵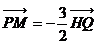
∴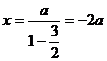
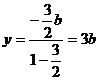
∴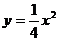 (2)解法一:设A(a,b),
(2)解法一:设A(a,b),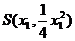 ,
,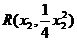 (x1≠x2)
(x1≠x2)
则:直线SR的方程为: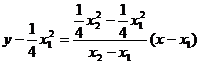 ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
对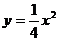 求导得:y′=
求导得:y′=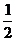 x
x
∴抛物线上S、R处的切线方程为:
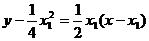 即4
即4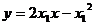 ②
②
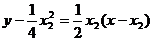 即4
即4 ③
③
联立②③,并解之得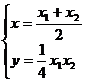 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0
故:B点在直线ax-2y-2b=0上
解法二:设A(a,b)
当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a)
与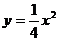 联立消去y得:x2-4kx+4ak-4b=0
联立消去y得:x2-4kx+4ak-4b=0
设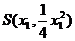 ,
,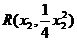 (x1≠x2)
(x1≠x2)
则由韦达定理: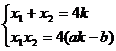
又过S、R点的切线方程分别为: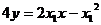 ,
,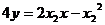
联立,并解之得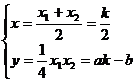 (k为参数)
(k为参数)
消去k,得:ax-2y-2b=0
故:B点在直线2ax-y-b=0上
22.解(1)令m=-1,n=0则:f(–1)=f(–1)f(0),而f(–1)>1 ∴f(0)=1
令m=x>0,n= –x<0则f(x–x)=f(x).f(–x)=1
∴f(x)=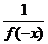
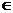 (0,1),即x>0时0<f(x)<1
(0,1),即x>0时0<f(x)<1
设x1<x2则x2–x1=0 ∴0<f (x2–x1).f (x1)–f (x1)=f (x1)[f (x2–x1)–1]<0 ∴f(x)<f(x1)
即y = f (x)在R上单调递减
(2)由f(an+1)=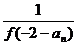 ,n
,n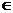 N*
得:f(an+1).f(–2–an) =1
N*
得:f(an+1).f(–2–an) =1
∴f(an+1–an–2) = f (0) 由(1)知:an+1–an–2=0
即an+1–an=2(n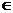 N*) ∴{an}是首项为a1=1,公差为2的等差数列
N*) ∴{an}是首项为a1=1,公差为2的等差数列
∴an=2n–1
(3)假设存在正数k,使(1+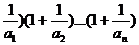
 对n
对n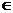 N*恒成立
N*恒成立
记F(n)=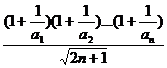
即 ∴F(n)是递增数列,F(1)为最小值。
∴F(n)是递增数列,F(1)为最小值。
由F(n)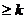 恒成立知k
恒成立知k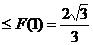 ∴kmax =
∴kmax = 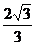 .
.