
网址:http://www.1010jiajiao.com/paper/timu/5142828.html[举报]
14.已知函数f(x)=,若方程f(x)=-2x有两个相等的实根,则函数解析式为 .
数 学(文科)参考答案
第Ⅱ卷(非选择题 共90分)
一.选择题 BBDBA DCBAC AA
二.填空题
13. -2 14. f(x)= 15. 48 16.①②③)
三.解答题
17.解:(1)∵=(sinB,1-cosB) ,与向量=(2,0)所成角为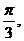
∴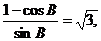 ……………………………………………………………3分
……………………………………………………………3分
∴tan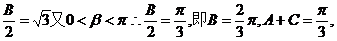 …………………6分
…………………6分
(2):由(1)可得∴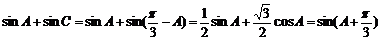
……………………………………8分
∵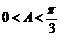
∴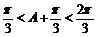 ……………………………………………………………………10分
……………………………………………………………………10分
∴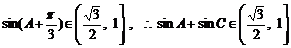
当且仅当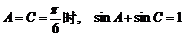 …………………………………12分
…………………………………12分
18.(1)∵(2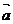 -3
-3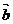 ).(2
).(2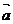 +
+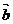 )=61,∴
)=61,∴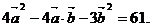 …2分
…2分
又|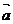 |=4,|
|=4,|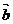 |=3,∴
|=3,∴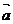 .
.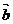 =-6.…………………………………………4分.
=-6.…………………………………………4分.
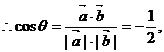 ………………………………………………5分
………………………………………………5分
∴θ=120°.………………………………………………………………6分
(2)设存在点M,且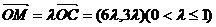
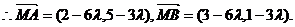
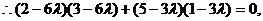 …………………………8分
…………………………8分
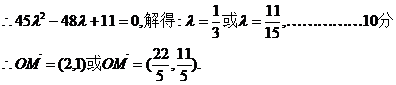
∴存在M(2,1)或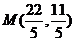 满足题意.……………………12分.
满足题意.……………………12分.
19.解:分别记该生语、数、英考试成绩排名全班第一的事件为A、B、C,则P(A)=0.9
P(B)=0.8,P(C)=0.85 …………………………2分
(1)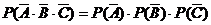
=[1-P(A)].[1-P(B)].[1-P(C)] =(1-0.9)×(1-0.8)×(1-0.85)=0.003
答:该生三科成绩均未获得第一名的概率是0.003………………6分
(2)P(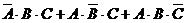 )
)
= P(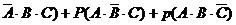
=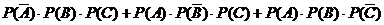
=[1-P(A)].P(B).P(C)+P(A).[1-P(B)].P(C)+P(A).P(B).[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)
=0.329
答:该生恰有一科成绩未获得第一名的概率是0.329……………………12分
20.∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1] 时,f(x)=f(x+2)=(x+2)-1=x+1.…………………………3分
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1,
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3.……………………………6分
设A、B的纵坐标为t(1≤t≤2),并设A在B的左边,则A、B的横坐标分别为
3-t,t+1.则|AB|=(t+1)-(3-t)=2t-2,△ABC的面积为S=.(2t-2).(a-t)
=-t2+(a+1)t-a=-(t-)2+ ……………………………………9分
∵2<a<3,∴<<2,∴当t=时,S有最大值.………12分
21.(1)∵2n+4=2+(n+2-1)d, ∴d=2,∴f(an)=2+(n+1-1).2=2n+2, ∴an=a2n+2.………3分
(2)Sn== .…………………………………………………7分
(3)∵bn=an.f(an)=(2n+2)a2n+2=(2n+2).22n+2=(n+1).22n+3 ,
∴= .4>1,∴bn+1>bn.………………………………………………12分
22.(1)∵,∴tanθ=.
又∵<m<4,∴1<m<4.………………………………6分
(2)设所求的双曲线方程为(a>0,b>0),Q(x1,y1),
则=(x1-c,y1),∴S△OFQ= ||.|y1|=2,∴y1=±.
又由.=(c,0).(x1-c,y1)=(x1-c)c=(-1)c2,∴x1=c.…………8分
∴||==≥.
当且仅当c=4时, ||最小,这时Q点的坐标为(,)或(,-).……12分
∴, ∴.
故所求的双曲双曲线方程为.…………………………………14分