
网址:http://www.1010jiajiao.com/paper/timu/5142851.html[举报]
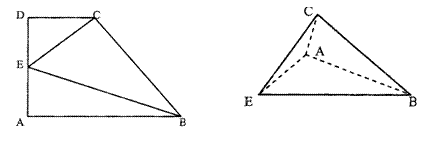
16.一直角梯形ABCD,AB⊥AD,AD⊥DC,AB=2,BC= ,CD=1,E为AD中点,沿
,CD=1,E为AD中点,沿
CE、BE把梯形折成四个面都是直角三角形的三棱锥,使点A、D重合,则这三棱锥的
体积等于 .
湖南师大附中高三第六次月考试卷
数学参考答案(理科)
一、选择题答案:
1.B 2.A 3.B 4.C 5.C 6.B 7.B 8.A 9.C 10.B 11.C 12.B
二、填空题答案:
13.-1,-1-2i
14.153.75元
15.56
16.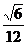
三、解答题
17.(1)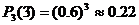
(2)
(3)
18.解①已知向量
若点A、B、C能构成三角形,则这三点不共线,………………2分
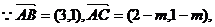 …………5分
故知
…………5分
故知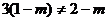 ……7分
……7分
∴实数 时,满足的条件…………8分
时,满足的条件…………8分
(若根据点A、B、C能构成三角形,必须|AB|+|BC|>|CA|…相应给分)
②若△ABC为直角三角形,且∠A为直角,则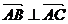 ,
,
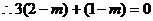 …………10分
解得
…………10分
解得 …………12分
…………12分
19.(1)证明:∵PB⊥底面ABC,∴PB⊥AC…………1分,又∠BCA=90°
∴AC⊥平面PBC…………4分
又AC 平面PAC,∴平面PAC⊥平面PBC…………5分
平面PAC,∴平面PAC⊥平面PBC…………5分
(2)解:设FE的延长线与AC的延长线交于M,连MB,
则MB为平面BEF与平面ABC的交线…………6分
在平面PCA中,由已知E是PC的中点,F是PA的四等分点,
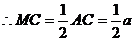 …………7分
…………7分
取BC的中点H,则EH//PB, ∴EH⊥底面ABC…………8分
过H作HO⊥MB于O,由三垂线定理,EO⊥MB
则∠EOH为平面BEF与底面ABC所成二面角的平面角…………9分
在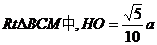 ,在
,在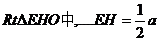 …………10分
…………10分
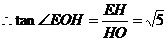 …………11分
…………11分
即平面BEF与底面ABC所成二面角的大小为 …………12分
…………12分
若利用面积射影法,指出△HDB是△EFB在底面ABC上的射影,并计算出其面积
 …………7分
计算出
…………7分
计算出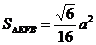 …………10分
…………10分
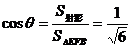 …………11分
…………11分
即平面BEF与底面ABC所成二面角的大小为 …………12分
…………12分
20.解(1)根据已知, ,
,
∴当n=1时, …………1分
…………1分
当n=2时,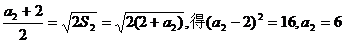 …………2分
…………2分
当n=3时,
 分别等于2,6,10…………3分
分别等于2,6,10…………3分
(2) …………4分
…………4分

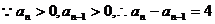 …………6分,由(1)
…………6分,由(1)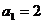 ,
,
 是以2为首项,4为公差的等差数列,
是以2为首项,4为公差的等差数列,
∴数列的通项公式 …………8分
…………8分
若用数学归纳法相应给分
(3)令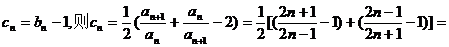
 …………10分
…………10分
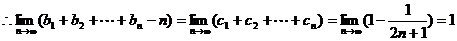 ……12分
……12分
21.解(1)∵函数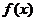 图象关于原点对称,∴对任意实数
图象关于原点对称,∴对任意实数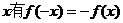 ,
,
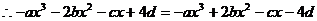 ,即
,即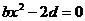 恒成立……1分
恒成立……1分
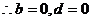 …………2分
…………2分
 ,
,
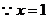 时,
时,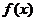 取极小值
取极小值 ,解得
,解得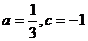 …4分
…4分
(2)当 时,图象上不存在这样的两点使结论成立.…………5分
时,图象上不存在这样的两点使结论成立.…………5分
假设图象上存在两点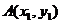 、
、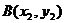 ,使得过此两点处的切线互相垂直,
,使得过此两点处的切线互相垂直,
则由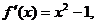 知两点处的切线斜率分别为
知两点处的切线斜率分别为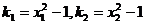 ,
,
且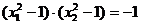 …………(*)…………7分
…………(*)…………7分
 、
、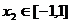 ,
,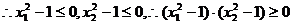
此与(*)相矛盾,故假设不成立.………………8分
证明(3) ,
,
或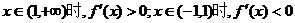 ,
,
 上是减函数,且
上是减函数,且 ……10分
……10分
∴在[-1,1]上,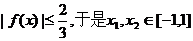 时,
时,
 .…………12分
.…………12分
22.解(1)由 …………1分
…………1分
又 ………2分
………2分
 ,故所求的轨迹方程是
,故所求的轨迹方程是 ……4分
……4分
(2)设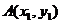 、
、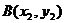 ,把
,把 ,得
,得
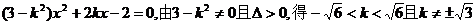 ……6分
……6分
∵A、B在y轴的同一侧, ,得到
,得到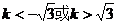 …………7分
…………7分
综上,得 .…………8分
.…………8分
(3)由(2)得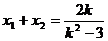 …………①
…………① 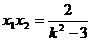 …………②
…………②
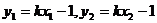 ……③………………9分
……③………………9分
∵曲线C与x轴交点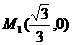 、
、 ,若存在实数k,符合题意,则
,若存在实数k,符合题意,则
 不妨取点
不妨取点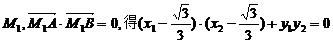 ……11分
……11分
将①②③式代入上式,整理得到 ,解得
,解得 舍去)……13分
舍去)……13分
根据曲线的对称性,知存在实数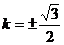 ,使得以AB为直径的圆恰好过M点…14分
,使得以AB为直径的圆恰好过M点…14分