
网址:http://www.1010jiajiao.com/paper/timu/5143088.html[举报]
19.(本小题满分12分)
如图所示,直三棱柱ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E为BB1的中点,点D在AB上且DE= .
.
(Ⅰ)求证:CD⊥面A1ABB1;
(Ⅱ)求二面角C-AE-D的大小;
(Ⅲ)求点A1到平面CDE的距离.
数学试题参考答案及评分标准(理科)
一、选择题:本题共12个小题,每小题5分,共60分.
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
B |
B |
A |
A |
C |
D |
C |
C |
D |
A |
B |
D |
二、填空题:本题共4个小题,每小题4分,共16分.
13.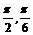 14.40 15.[0,2] 16.72
14.40 15.[0,2] 16.72
三、解答题:本题共6个小题,共74分.
17.(本小题满分12分)
解:(Ⅰ)∴ =(sinα,1)共线
t
=(sinα,1)共线
t
∴sinα+cosα=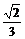 ……………………………………………………………… 2分
……………………………………………………………… 2分
故sin2α=-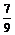
从而(sinα-cosα)2=1-sin2α=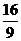 ……………………………………………… 4分 x
……………………………………………… 4分 x
∴α∈(- )∴sinα<0,cosα>0
)∴sinα<0,cosα>0
∴sinα-cosα=- …………………………………………………………………6分
…………………………………………………………………6分
(Ⅱ)∵ =2cos2α=1+cos2α……9分
=2cos2α=1+cos2α……9分
又cos2α=cos2α-sin2α=(cosα+sinα)(cosα-sinα)=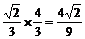
∴原式=1+ …………………………………………………………………… 12分
…………………………………………………………………… 12分
18.(本小题满分12分)
解:(Ⅰ)由题意知,从甲袋中摸出白球和从乙袋中摸出红球是相互独立的,则
P=C .
. .(
.(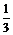 )2.C
)2.C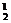 .
.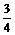 .
.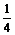 =
= ………………………………………………3分
………………………………………………3分
(Ⅱ)由题意知,事件A:从甲袋中摸出白球2次,从乙袋中摸出白球0次;事件B:从甲、乙袋中摸出白球各1次,事件C:从甲袋中摸出白球0次,从乙袋中摸出白球2次,则
P(A)=C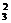 .(
.( )2.
)2.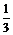 .C
.C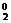 .(
.(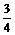 )0.(
)0.(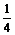 )2=
)2= ……………………………………… 5分
……………………………………… 5分
P(B)=C .
. .(
.(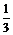 )2.C
)2.C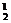 .
.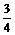 .
.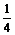 =
= …………………………………………… 7分
…………………………………………… 7分
P(C)=C .(
.( )0(
)0(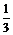 )3.C
)3.C (
(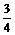 )2(
)2(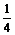 )0=
)0= …………………………………………9分
…………………………………………9分
又事件A、B、C互斥
∴所求事件的概率为:
P(A)+P(B)+P(C)=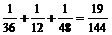 ………………………………………………10分
………………………………………………10分
(Ⅲ)由题意知,随机变量ζ服从二项分布ζ~B(3, )
)
∴Eζ=3× =2……………………………………………………………………
12分
=2……………………………………………………………………
12分
19.(本小题满分12分)
解:(Ⅰ)∵ABC-A1B1C1为直三棱柱
∴B1B⊥AB,又BE=1,DE=
∴BD=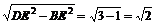
又AB=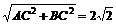 ……………………………………………………………2分
……………………………………………………………2分
∴D为AB中点,由于AC=BC
∴CD⊥AB.
由已知,面ABB1A1⊥面ABC
∴CD⊥面A1ABB1……………………………………………………………………4分
(Ⅱ)由(Ⅰ)知CD⊥面A1ABB1,过D作DF⊥AE于F,连FC,则FC⊥AE,
故∠DFC为二面角C-AE-D的平面角………………………………………… 6分
∵BE=1,AB=2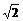 ,AE=
,AE=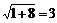
在Rt△ABE中
,sin∠DAE=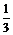
在Rt△ADF中,DF=AD.sin∠DAE=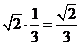
在Rt△CDF中,tan∠DFC=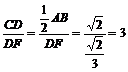
∴∠DFC=arctan3
即二面角C-AE-D大小为arctan3. …………………………………………………9分
(Ⅲ)连接A1D、A1E,∵A1B1=2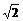 ,AA1=2,AD=
,AA1=2,AD=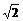 ,B1E=1
,B1E=1
∴A1E=3,A1D= ,
,
又DE= ,∴A1D⊥DE.
,∴A1D⊥DE.
又∵CD⊥平面A1ABB1,∴CD⊥A1D.
故A1D⊥平面CDE,即A1D为点A1到平面CDE的距离
∴点A1到平面CDE的距离为 .…………………………………………………
12分
.…………………………………………………
12分
20.(本小题满分12分)
解:(Ⅰ)当a=1时,f′(x)=e-x(-x2+x)
当f′(x)>0时,0<x<1
当f′(x)0<时,x>1或x<0
所以,f(x)的单调递增区间为(0,1),单调递减区间为(-∞,0),(1,+∞) ……4分
(Ⅱ)f′(x)=(2x+a)e-x-e-x(x2+ax+a)=e-x[-x2+(2-a)x]
令f′(x)=0,得x=0或x=2-a…………………………………………………………6分
列表如下:
|
x |
(-∞,0) |
0 |
(0,2-a) |
2-a |
(2-a,+∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
极小 |
↗ |
极大 |
↘ |
由表可知f极大(x)=f(2-a)=(4-a)ea-2…………………………………………………8分
设g(a)=(4-a)ea-2
g′(a)=-ea-2+ea-2(4-a)=(3-a).ea-2>0
∴g(a)在(-∞,2]上是增函数…………………………………………………… 10分
∴g(a)<g(2)=2<3
∴(4-a)ea-2≠3
∴不存在实数a,使得f(x)的极大值为3. ……………………………………… 12分
21.(本小题满分12分)
解:(Ⅰ)设点C,G的坐标分别为(x,y),(x0,y0),
 =(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)
=(-1-x0,-y0)+(1-x0,-y0)+(x-x0,y-y0)
=(x-3x0,y-3y0)=
∴ ……………………………………………………………2分
……………………………………………………………2分
由 和
和 ∥
∥ ,知点M的坐标为(0,y0),
,知点M的坐标为(0,y0),
由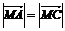 ,可得
,可得 ,
,
∴1+ ,
,
即x2+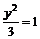 ,
,
故点C的轨迹方程是x2+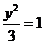 (y≠0).
………………………………………… 5分
(y≠0).
………………………………………… 5分
(Ⅱ)直线l的斜率为k(k≠0),则它的方程为y=k(x-2),
由 可得(3+k2)x2-4k2x+4k2-3=0,
可得(3+k2)x2-4k2x+4k2-3=0,
其中△=16k2-4(3+k2)(4k2-3)=36(1-k2)>0,
∴-1<k<1且k≠0……………………………………………………………………7分
设两交点E,F的坐标分别为(x1,y1),(x2,y2),由韦达定理得
x1+x2= ,x1.x2=
,x1.x2= ……………………………………………………… 8分
……………………………………………………… 8分
又因为y1=k(x1-2),y2=k(x2-2),从而
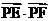 =(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)
=(1+k2)( )=
)=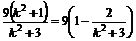 …………… 10分
…………… 10分
又0<k2<1,所以3<k2+3<4,得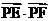 ∈(3,
∈(3,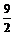 ).
).
∴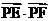 的取值范围是(3,
的取值范围是(3,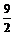 ).…………………………………………………12分
).…………………………………………………12分
22.(本小题满分14分)
解:(Ⅰ)由已知,当n=1时,a ,∵a1>0,∴a1=1.
………………………… 1分
,∵a1>0,∴a1=1.
………………………… 1分
当n≥2时, …+
…+ ①
①
 …+
…+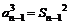 ②
②
由①-②得,a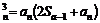 ……………………………………………………3分
……………………………………………………3分
∵an>0,
∴a =2Sn-1+an,即a
=2Sn-1+an,即a =2Sn-an,
=2Sn-an,
当n=1时,∴a1=1适合上式,
∴a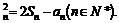 ………………………………………………………5分
………………………………………………………5分
(Ⅱ)由(Ⅰ)知,a ,即a
,即a =2Sn-an(n∈
=2Sn-an(n∈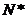 )③
)③
当n≥2时,a =2Sn-1-an-1
④
=2Sn-1-an-1
④
由③-④得,
a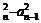 =2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1…………………………………… 8分
=2(Sn-Sn-1)-an+an-1=2an-an+an-1=an+an-1…………………………………… 8分
∵an+an-1>0,∴an-an-1=1,数列{an}是等差数列,首项为1,公差为1,
可得an=n. …………………………………………………………………………10分
(Ⅲ)∵an=n,∴bn=3n+(-1)n-1λ.2an=3n+(-1)n-1λ.2n, …………………………11分
要使bn+1> bn恒成立,
bn+1-bn=3n+1+(-1)nλ.2n+1-[3n+(-1)n-1λ.2n]
=2.3n-3λ(-1)n-1.2n>0恒成立
则(-1)n-1.λ<( )n-1恒成立……………………………………………………12分
)n-1恒成立……………………………………………………12分
当n为奇数时,即为λ<( )n-1恒成立
)n-1恒成立
又( )n-1的最小值为1,
)n-1的最小值为1,
∴λ<1
当n为偶数时,即为λ>-( )n-1恒成立
)n-1恒成立
又-( )n-1最大值为-
)n-1最大值为-
∴λ>- …………………………………………………………………………… 13分
…………………………………………………………………………… 13分
∴- <λ<1,又λ≠0,∴λ=-1
<λ<1,又λ≠0,∴λ=-1
∴λ=-1,使得对任意n∈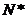 ,都有bn+1>bn……………………………………
14分
,都有bn+1>bn……………………………………
14分