
网址:http://www.1010jiajiao.com/paper/timu/5143097.html[举报]
7.圆心在抛物线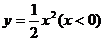 上,并且与抛物线的准线及y轴都相切的圆的方程为( )
上,并且与抛物线的准线及y轴都相切的圆的方程为( )
A.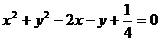 B.
B.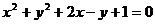
C.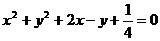 D.
D.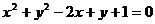
数学参考答案
一、选择题
1.D 2.B 3.B 4.C 5.C 6.A 7.C 8.B 9.A 10.C 11.B 12.D
二、填空题
13.15、2、3 14.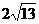 15.
15. (注:未写x的取值范围可视作正确) 16.1或
(注:未写x的取值范围可视作正确) 16.1或
三、解答题
17.(1)经过各交叉路口遇到红灯,相当于独立重复试验,所以恰好遇到3次红灯的概率为
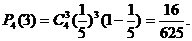 …………6分
…………6分
(2)记“经过交叉路口遇到红灯”事件A.
张华在第1、2个交叉路口末遇到红灯,在第3个交叉路口遇到红灯的概率为
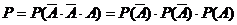 …………10分
…………10分
=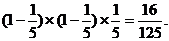 …………12分
…………12分
18.(1)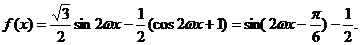 …………3分
…………3分
由函数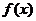 的周期
的周期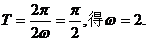 …………5分
…………5分
函数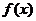 的表达式为
的表达式为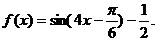 …………6分
…………6分
(2)由题意,得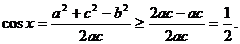 …………8分
…………8分
又 ∴
∴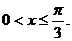 …………9分
…………9分
∴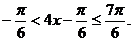 ………………10分
………………10分
∴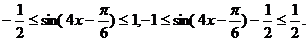
即函数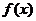 的值域为[-1,
的值域为[-1,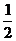 ].…………12分
].…………12分
19.解答一:
(1)PA与BD相互垂直.证明如下:
|
连结PO.…………1分 ∵PB=PC,∴PO⊥BC.
又∵平面PBC⊥平面ABCD,
平面PBC∩平面ABCD=BC,
∴PO⊥平面ABCD.…………2分
在梯形ABCD中,可得Rt△ABO≌Rt△BCD,
∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,
即AO⊥BD. ∴PA⊥BD. …………4分
(2)连结PE,由PO⊥平面ABCD,AO⊥BD,可得PE⊥BD,…………5分
∴∠PEO为二面角P-BD-C的平面角.………………6分
设AB=BC=PB=PC=2CD=2a,则在Rt△PEO中,PO=
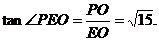 ∴二面角P-BD-C为
∴二面角P-BD-C为 …………8分
…………8分
(3)取PB的中点N,连结CN,由题意知:平面PBC⊥平面PAB,则同“(1)”可得CN⊥平面PAB. ………………9分
取PA的中点M,连结DM、MN,则由MN//AB//CD,MN=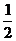 AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
AB=CD,得四边形MNCD为平行四边形. ∴CN//DM. …………10分 ∴DM⊥平面PAB.…………11分
∴平面PAD⊥平面PAB.………………12分
解答二:
|
△PBC是等边三角形,
得PO⊥底面ABCD.…………1分
以BC中点O为原点,以BC所在直线为x轴,
过点O与AB平行的直线为y轴,
建立如图所示的空间直角坐标系O-xyz.……2分
设CD=1,则在直角梯形中,AB=BC=2,
在等边三角形PBC中,PO= .…………3分
.…………3分
∴A(1,-2,0),B(1,0,0)、D(-1,-1,0)、
P(0,0, ).
).
 …………4分
…………4分
(1)PA与BD相互垂直.证明如下:∵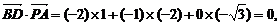
∴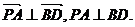 …………6分
…………6分
(2)连结AO,设AO与BD相交于点E;连结PE.
由 得
得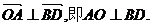
又∵AO为PA在平面ABCD内的射影,
∴PE⊥BD,∠PEO为二面角P-BD-C的平面角.…………8分
在Rt△BEO中,OE=OB.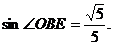
在Rt△PEO中,
∴二面角P-BD-C为 ……9分
……9分
(3)取PA的中点M,连结DM,则M的坐标为(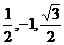 ).……10分
).……10分
又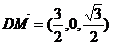 ,
,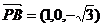 ,
,
∴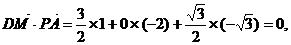
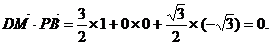
∴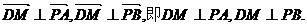 ………………11分
………………11分
∴DM⊥平面PAB. ∴平面PAD⊥平面PAB.…………12分
20.(1)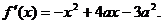 …………1分
…………1分
令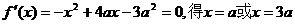 …………2分
…………2分
由表
|
x |
|
a |
|
3a |
|
||
|
f′ |
- |
0 |
+ |
0 |
- |
||
|
f |
递减 |
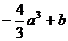 |
递增 |
b |
递减 |
可知:当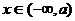 时,函数
时,函数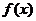 为减函数,当
为减函数,当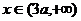 时。函数
时。函数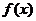 也为减函数;当
也为减函数;当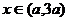 时,函数
时,函数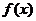 为增函数.…………5分
为增函数.…………5分
当x=a时,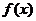 的极小值为
的极小值为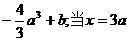 时,
时,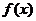 的极大值为b.……6分
的极大值为b.……6分
(2)由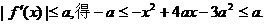 ……7分
……7分
∵0<a<1, ∴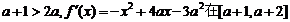 上为减函数.……8分
上为减函数.……8分
∴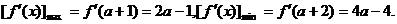 …………9分
…………9分
于是,问题转化为求不等式组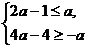 的解.…………10分
的解.…………10分
解不等式组,得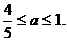 …………11分
…………11分
又0<a<1, ∴所求a的取值范围是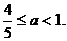 …………12分
…………12分
21.(1)当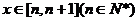 时,函数
时,函数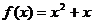 的值随x的增大而增大,则
的值随x的增大而增大,则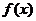 的值域为
的值域为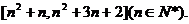 …………2分
…………2分
∴ …………3分
…………3分
(2)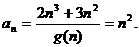 …………4分
…………4分
①当n为偶数时,

=-[3+7+……+(2n-1)]=-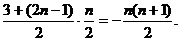 …………6分
…………6分
②当n为奇数时,

=- ………………8分
………………8分
∴
(3)由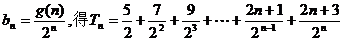 , ①
, ①
①×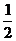 ,得
,得 ②…………9分
②…………9分
①-②,得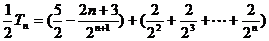
=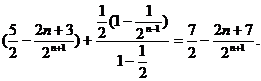
∴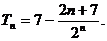 ………………11分
………………11分
则由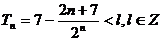 ,可得l的最小值是7.…………12分
,可得l的最小值是7.…………12分
22.(1)由题意知: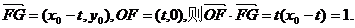 ………1分
………1分
解得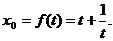 …………2分
…………2分
设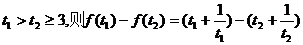
=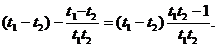
∵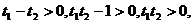 ∴
∴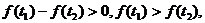
函数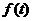 在区间[3,+∞)上单调递增.…………4分
在区间[3,+∞)上单调递增.…………4分
(2)由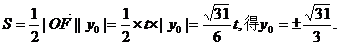 …………5分
…………5分
∴点G的坐标为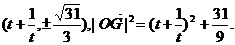 …………6分
…………6分
∵函数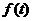 在区间[3,+∞]上单调递增,
在区间[3,+∞]上单调递增,
∴当t=3时,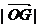 取得最小值,此时点F、G的坐标分别为
取得最小值,此时点F、G的坐标分别为
(3,0)、(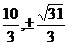 ).……7分
).……7分
由题意设椭圆方程为 …………8分
…………8分
由点G在椭圆上,得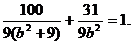 解得b2=9.
解得b2=9.
∴所求椭圆方程为 …………10分
…………10分
(3)解答一:设C、D的坐标分别为(x,y)、(m,n),
则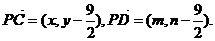
由 ………11分
………11分
∵点C、D在椭圆上,∴
消去m,得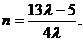 …………12分
…………12分
又∵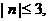 ∴
∴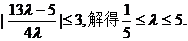 …………13分
…………13分
∴实数λ的取值范围是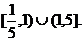 …………14分
…………14分
解答二:设点A、B的坐标分别为(0,3)、(0,-3),过点A、B分别作y轴的垂线,交直线PC于点M、N.
若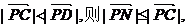 ∴1
∴1
则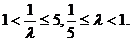 …………12分
…………12分
若 同理可得
同理可得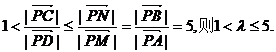 ……13分
……13分
综上,实数λ的取值范围是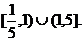 …………14分
…………14分