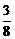16.
①对,如图,顶点P在底面上的射影为底面中心O. ∵AC⊥BD, ∴PA⊥BD,即PA与BD所成的角为直角.
②对,设正四棱锥底面边长为a,侧棱长为b, 则AC=a,OA=OB=a.
∵b>a,在△PAB中,PA2+PB2-AB2=2b2-a2>2(a)2-a2=0,
∴∠APB为锐角,故△APB为锐角三角形,即侧面为锐角三角形.
③对,取BC中点E,连PE、OE,易知∠PEO为侧面与底面所成的角,∠PBO为侧棱与底面所成的角,sin∠PEO=,sin∠PBO=. ∵PB>PE,
∴sin∠PEO>sin∠PBO. ∴∠PEO>∠PBO.
④对,作AF⊥PB于F,连FC,易证FC⊥PB, ∴∠AFC为相邻两侧面所成的二面角.
∵AF<AB,CF<BC,在△AFC中,AF2+CF2-AC2<AB2+BC2-AC2=0,从而∠AFC>90°.
故相邻两侧面所成的二面角为钝角.
答案: ①②③④

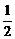 ×
×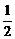 ×
×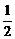 =
=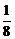 .
.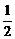 ×(
×(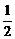 ×
×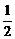 +
+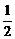 ×
×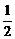 +
+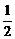 ×
×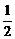 )=
)=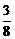 . 答案:
. 答案: 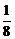 ,
,