
网址:http://www.1010jiajiao.com/paper/timu/5143484.html[举报]
14.设函数f(x)=lg(x2+ax-a-1),给出下列命题:①f(x)有最小值;②当a=0时,f(x)值域为R;③当a>0时,f(x)在[2,+∞)上有反函数;④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围是a≥-4,其中正确命题的序号为______.
参考答案
一、选择题
1.C M=2-1=1,m=-2-1=-3,∴M+n=1-3=-2.
2.B M=(0,1),N=(-2,2),M∩n=(0,1)=M.
3.C 由定义域知x<1,故排除A、B,由函数单调递减,故选C.
4.A 椭圆方程为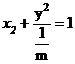 ,由题意得
,由题意得 =2×1,∴m=4.
=2×1,∴m=4.
5.A 设S4=m,则S8=3m,∴S8-S4=2m,由等差数列性质知,S12-S8=3m,S16-S12=4m,∴S16=10m,∴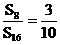 .
.
6.D 设直线L平行于直线y=2y+1,且与曲线y=x4相切于点P(x0,y0),则所求最小值d,即点P到直线y=2y+1的距离,y′=4x3=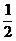 .
.
∴x0=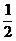 ,y0=
,y0=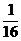 .
.
∴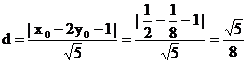 .
.
7.C 设PB=PC=AB=BC=AC=2,则当面PBC⊥面ABC时,四面体PABC体积最大,V=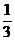 .
.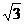 .
.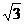 =1.
=1.
8.D 代入检验知直线过定点(-1,1).
9.B 分别将0,1,2,3……8放在十位上,则凹数个数为
 92+82+72+…+12=
92+82+72+…+12=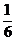 ×9×(9+1)×(2×9+1)=285.
×9×(9+1)×(2×9+1)=285.
10.D 由L与C方程消x得y2-2y0y+4x0=0(*),Δ=4y02-16x0=4(y02-4x0)<0.
∴方程(*)无实根,∴l与C无公共点.
二、填空题
11.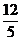 ∵a.b=|a||b|cosθ=12,|b|=5,∴|a|cosθ=
∵a.b=|a||b|cosθ=12,|b|=5,∴|a|cosθ=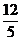 .
.
12.200
13.75 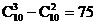 .
.
14.②③
三、解答题
15.解:(1)∵a=(cosα,sinα),b(cosβ,sinβ),
∴a-b=(cosα-cosβ,sinα-sinβ). 2分
∵|a-b|= ,
,
∴ ,
4分
,
4分
即2-2cos(α-β)= .∴cos(α-β)
.∴cos(α-β)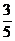 .
7分
.
7分
(2)∵0<α<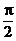 ,
,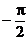 <β<0,∴0<α-β<π.
9分
<β<0,∴0<α-β<π.
9分
∵cos(α-β)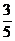 ,∴sin(α-β)=
,∴sin(α-β)= . sinβ=
. sinβ= ,∴cosβ=
,∴cosβ= . 12分
. 12分
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ= .
. +
+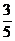 .(
.( )=
)= .
14分
.
14分
16.解:记“第一套通讯设备能正常工作”为事件A,“第二套通讯设备能正常工作”为事件B,由题意知
P(A)=p3,P(B)=p3. 2分
P( )=1-p3,P(
)=1-p3,P(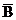 )=1-p3.
)=1-p3.
(1)恰有一套设备能正常工作的概率为P(A.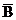 +
+ .B)=P(A.
.B)=P(A.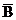 )P(
)P( .B) 4分
.B) 4分
=p3(1-p3)+(1-p3)p3=2p3-2p6. 7分
(2)解法一:两套设备都能正常工作的概率为P(A.B)=P(A).P(B)=p6. 9分
至少有一套设备能正常工作的概率,即能进行通讯的概率为P(A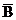 +
+ B)+P(AB)=2P3-2P6+P6=2P3-P6.
13分
B)+P(AB)=2P3-2P6+P6=2P3-P6.
13分
解法二:两套设备都不能正常工作的概率为P( .
.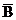 )=P(
)=P( ).P(
).P(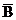 )=1(1-p3)2.
)=1(1-p3)2.
9分
至少有一套设备能正常工作的概率,即能进行通讯的概率为
1-P( .
.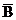 )=1-P(
)=1-P( ).P(
).P(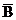 )=1(1-p3)2=2p3-p6.
13分
)=1(1-p3)2=2p3-p6.
13分
答:恰有一套设备能正常工作的概率为2p3-2p6,能进行通讯的概率为2p3-p6. 14分
17.解:(1)当BC<2时,不存在;当BC=2时,存在唯一;当BC>2时,存在两个.
4分
(2)此时,BC=2,Q为BC中点,连AQ,作AE⊥PQ于E.
∵DQ⊥PA,DQ⊥PQ,∴DQ⊥面PAQ.∴PDQ⊥面PAQ.∴AE⊥面PDQ,AE=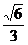 ,AD=2,sinθ=
,AD=2,sinθ= 即正弦值为
即正弦值为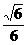 .
9分
.
9分
(3)∵PA⊥面ABCD,AB⊥DA,AB⊥BC,
BC面PBA,DA⊥面PBA,cosθ=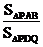 .
11分
.
11分
S△PAB=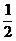 .1.1=
.1.1=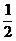 ,S△PDQ=
,S△PDQ=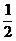 .
. .
.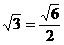 .
.
∴cosθ ,即大小为arccos
,即大小为arccos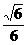 .
14分
.
14分
18.解:(1)f′(x)=-x2+4ax-3a2.
令f′(x)=-x2+4ax-3a2=0,
得x=a或x=3a. 2分
由表
|
x |
|
a |
|
3a |
|
|
y′ |
- |
0 |
+ |
0 |
- |
|
y |
递减 |
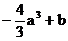 |
递增 |
b |
递减 |
可知:当x∈(-∞,a)时,函数f(x)为减函数;
当x∈(3a,+∞)时,函数f(x)也为减函数;
当x∈(a,3a)时,函数f(x)为增函数; 4分
当x=a时,f(x)的极小值为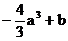 ;
;
当x=3a时,f(x)的极大值为b; 7分
(2)由|f′(x)|≤a,得-a≤-x2+4ax-3a2≤a.
∵0<a<1,
∴a+1>2a,f′(x)=-x2+4ax-3a2,在[a+1,a+2]上为减函数. 10分
∴[f′(x)]max=f′(a+1)=2a-1,
[f′(x)]min=f′(a+2)=4a-4.
于是,问题转化为求不等式组 的解.
的解.
解不等式组,得 ≤a≤1.
≤a≤1.
又0<a<1,∴所求a的取值范围是 ≤a≤1.
14分
≤a≤1.
14分
19.解:(1)①q=1时,不存在C. 2分
②Sn=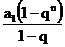 (q≠1),Sn
(q≠1),Sn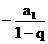 =
=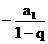 .qn.
.qn.
∴C=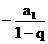 .
6分
.
6分
(2)①当q=1时,S3=3q1,S8=8q1,S9=9q1,不合题意. 8分
②当q≠1时,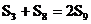 ,
,
∴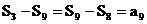 ,
,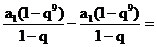
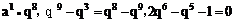 .
.
∴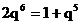 且q≠1,又
且q≠1,又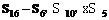 成等比数列,
成等比数列,
∴S102=xS5(S16-S6). 10分
∴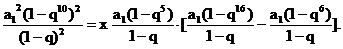
∴(1-q10)2=x(1-q5)(q6-q16).
∴1+q5=xq6,又2q6=1+q5.
∴2q6=xq6,而且q≠0.∴x=2. 14分
20.解:(1)由题意知 ,
,
 ,则
,则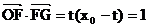 .
.
解得 .
.
设t1>t2≥3,则
∵t1-t2>0,t1t2-1>0,t1t2>0,
∴f(t1)-f(t2)>0,f(t1)>f(t2),
函数f(t)在区间[3,+∞]上单调递增. 4分
(2)由S= 得y0=
得y0= .
.
∴点Q的坐标为(t+
 ),
),
∵函数f(t)在区间[3,+∞]上单调递增,
∴当t=3时, 取得最小值,此时点F、G的坐标分别为(3,0)、(
取得最小值,此时点F、G的坐标分别为(3,0)、(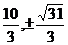 ).
).
由题意设椭圆方程为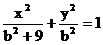 .
.
由点G在椭圆上,得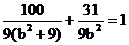 ,解得b2=9.
,解得b2=9.
∴所求椭圆方程为 .
8分
.
8分
(3)设C、D的坐标分别为(x,y)、(m,n),则 .
.
由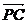 =
=
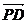 ,得
,得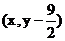 =
=
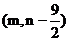 ,x=
,x= m,y=
m,y= n-
n-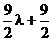 .
.
∵点C、D在椭圆上,
∴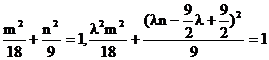 .
.
消去m,得n=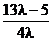 .
.
又∵|n|≤3,∴|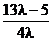 |≤3,解得
|≤3,解得 ≤
≤ ≤5.
≤5.
∴实数 的取值范围是
的取值范围是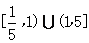 .
14分
.
14分