
网址:http://www.1010jiajiao.com/paper/timu/5143709.html[举报]
12.对于集合 、
、 ,定义
,定义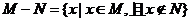 ,
, 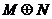 =
=

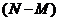 .设
.设 ,
,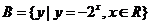 ,则
,则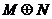 =( )
=( )
A. B.
B.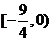 C.
C. D.
D.
参考答案
一、选择题(60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
D |
A |
D |
C |
B |
C |
B |
D |
A |
A |
C |
C |
二、填空题(16分)
13.200
14.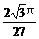 15.
15.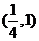 16.a<c<b
16.a<c<b
三、解答题
17.解:(1)令n=(x,y),则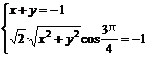
即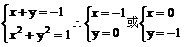 ,故n=(-1,0)或n=(0,-1)
,故n=(-1,0)或n=(0,-1)
(2)∵a=(1,0)n.a=0
∴n=(0,-1) n+b=
故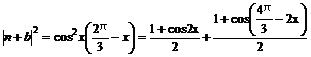 =1+
=1+
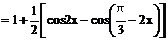 =1+
=1+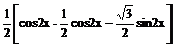
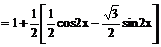 =1+
=1+
∵0<x<
则-1≤cos
18.解:⑴红色骰子投掷所得点数为 是随即变量,其分布如下:
是随即变量,其分布如下:

 8 2
8 2
P 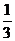
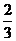
E =8.
=8.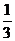 +2.
+2.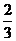 =4
=4
蓝色骰子投掷所得点数 是随即变量,其分布如下:
是随即变量,其分布如下:

 7 1
7 1
P 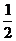
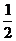
E =7.
=7.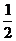 +1.
+1.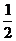 =4
=4
⑵∵投掷骰子点数较大者获胜,∴投掷蓝色骰子这若获胜,则投掷后蓝色骰子点数为7,
红色骰子点数为2,∴投掷蓝色骰子获胜概率是 =
=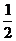 .
.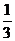 =
=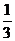
19.解:(1)建立如图所示的空间直角坐标系,则A (a,0,0) , B(a,a,0),
C(0,a,0),P(0,0,a)
 。
。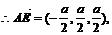
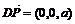 。
。
 。 又
。 又
 。故异面直线AE、DP所成角为
。故异面直线AE、DP所成角为 。
。
(2)∵F∈平面PAD,故设F(x,0,z),则有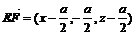 。
。
∵EF⊥平面PBC,∴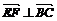 且
且 。∴
。∴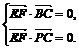
又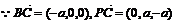 ,
,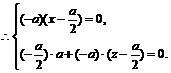
从而 ∴
∴ ,取AD的中点即为F点。
,取AD的中点即为F点。
(3)∵PD⊥平面ABCD, ∴CD是PC在平面ABCD上的射影。
又∵CD⊥BC,由三垂线定理,有PC⊥BC。取PC的中点G,连结EG,则EG//BC。
∴EG⊥PC。连结FG。∵EF⊥平面PBC,EG是FG在平面PBC上的射影,且PC⊥EG,∴FG⊥PC。∴∠FGE为二面角F―PC―E的平面角。 。
。 。∴二面角F―PC―E的大小为
。∴二面角F―PC―E的大小为 。
。
20.解: ,
,
⑴ 函数
函数 的图象有与
的图象有与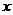 轴平行的切线,
轴平行的切线,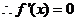 有实数解
有实数解
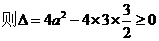 ,
,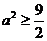 ,所以
,所以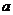 的取值范围是
的取值范围是
⑵ ,
,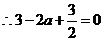 ,
,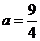 ,
,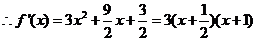
(Ⅰ)由 或
或 ;由
;由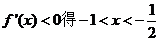
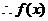 的单调递增区间是
的单调递增区间是 ;单调减区间为
;单调减区间为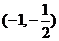
(Ⅱ)易知 的最大值为
的最大值为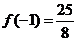 ,
, 的极小值为
的极小值为 ,又
,又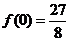
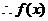 在
在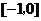 上的最大值
上的最大值 ,最小值
,最小值
 对任意
对任意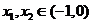 ,恒有
,恒有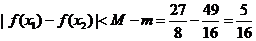
21.解:(1)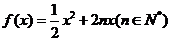 ;(2)
;(2) ;
;
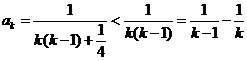 (
( )当
)当 时,显然成立;
时,显然成立;
当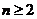 时,
时, ;
;
22.解:(1)由条件得直线AP的方程为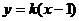 ,即
,即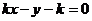 ,
,
∵点M到直线AP的距离为1,
∴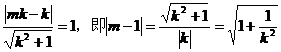 ,………………………………… 3分
,………………………………… 3分
∵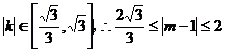 ,
,
即 ,或
,或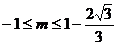 ,
,
∴m的取值范围是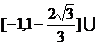
 .…………………………………… 6分
.…………………………………… 6分
(2)可设双曲线的方程为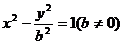 ,……………………………………… 7分
,……………………………………… 7分
∵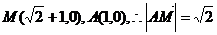 ,
,
∵M是△APQ的内心,且M到直线AP的距离为1,∴∠MAP=45°,………… 9分
即直线AM是∠PAQ的角平分线,不妨设P在第一象限,
则直线AP、AQ的斜率分别为kAP=1,kAQ=-1,……………………………………… 10分
又由双曲线的对称性及点M到PQ的距离为1知直线PQ的方程为
再联立直线AP的方程 得点
得点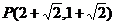 ,……………………… 11分
,……………………… 11分
将点P的坐标代入双曲线的方程得
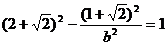 ,解得
,解得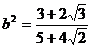 ,……………………………… 12分
,……………………………… 12分
即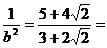
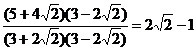 ,…………………………… 13分
,…………………………… 13分
∴双曲线的方程为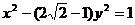 .………………………………………… 14分
.………………………………………… 14分