
网址:http://www.1010jiajiao.com/paper/timu/5144835.html[举报]
18、(本题满分12分)
已知a = (cos2x,sin2x),
b = (cosx,-sinx), c = (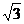 ,-1),其中
,-1),其中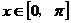 ;
;
(1)当a∥b时,求x的值的集合;
(2)设f(x) = |a - c|2,求f(x)的单调递增区间。
乐山市高中2006届第一次诊断考试数学(理)参考答案
2006.1
一、选择题:ACDCDD CDAACB
二、填空题:13、a -1 14、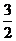 15、2 16、6
15、2 16、6
三、解答题
17、解:(1)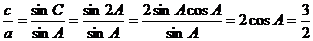
(2)由a+c=10,及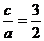 得到a=4,c=6
得到a=4,c=6
又因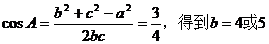
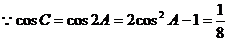
当b=4时,此时C>90°不合题意,舍去
\ b=5
18、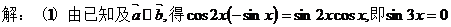
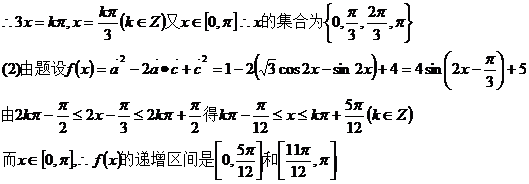
19、解:(Ⅰ)由题意,有 (a1+d)(a1+13d)=(a1+4d)2.
而a1=1, d>0,∴d=2.
∴an=2n-1.
公比q=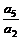 =3,a2=b2=3.
=3,a2=b2=3.
∴bn=b2.qn-2=3.3n-2= 3n-1.
(Ⅱ)当n=1时,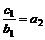 ,∴c1=1×3=3.
,∴c1=1×3=3.
当n≥2时,
∵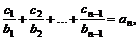 ……①
……①
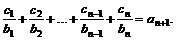 ……②
……②
②-①,得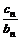 =an+1-an=2,
=an+1-an=2,
∴cn=2bn=2.3n-1(n≥2).
即有cn=
∴c1+ c2+ c3+…+ c2006=3+2(31+32+33+…+32005)
=3+2.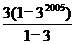 =32006.
=32006.
20、解:(1)应用二元均值不等式,得
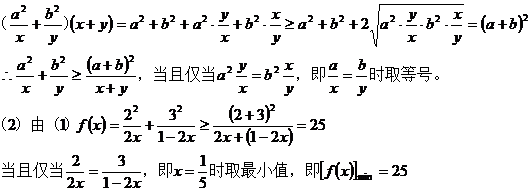
21、解:(1)
|
国徽面朝上次数m |
3 |
2 |
1 |
0 |
||
|
P(m) |
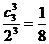 |
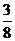 |
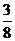 |
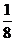 |
||
|
国徽面朝上次数n |
2 |
1 |
0 |
|||
|
P(n) |
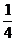 |
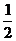 |
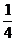 |
|||
(2)这种规定是合理的。因为甲胜,则m > n,当m=3时,n=2,1,0
其概率为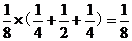
当m=2时,n=1,0,其概率为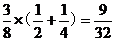
当m=1时,n=0,其概率为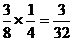 ,\甲获胜的概率为
,\甲获胜的概率为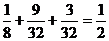
乙获胜,则m £ n,当n=2时,m=2,1,0,其概率为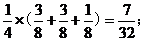
当n=1时,m=1,0,其概率为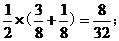
当n=0时,m=0,其概率为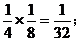
\乙获胜的概率为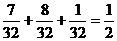
22、(Ⅰ)解:

即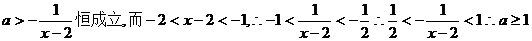
(Ⅱ)证明:由题设知,a1 Î(0,1),令0<ak<1,当n=k+1时,ak+1 = ln(2-ak)+ak>0
ak+1 = ln(2-ak)+ak<1,(由第一问知函数f (x) = ln (2-x) + x在(0,1)上是增函数)
所以0< an <1, nÎN* 又因为an+1 – an = ln(2 - an) > 0所以0< an < an+1 <1
(Ⅲ)数列{bn}不具有单调性.令g (x) = 2ln(2-x)+x
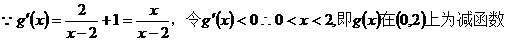
∵b1 Î(0,1),b2 = 2ln(2-b1)+b1\2ln1+1<b2<2ln2+0 ∴1< b2 < 2ln2 < 2
b3= 2ln(2-b2)+b2 ,∴b3<2ln1+1 =1 即有: b1 < b2 , b2 > b3
∴数列{bn}不具有单调性