
网址:http://www.1010jiajiao.com/paper/timu/5144899.html[举报]
17.已知函数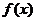 是定义在
是定义在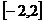 上的奇函数,当
上的奇函数,当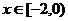 时,
时,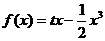 (
(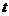 为常数)
为常数)
(1)求函数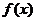 的解析式;
的解析式;
(2)当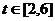 时,求
时,求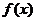 在
在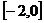 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的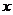 ,并猜想
,并猜想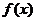 在
在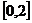 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当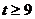 时,证明:函数
时,证明:函数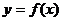 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线 上
上
答案:
1 B 2
B 2 B 3
B 3 A 4
A 4 B 5
B 5 A
A
6 B 7
B 7 C 8
C 8 B 9
B 9 D 10
D 10 D
D
11
 12
12
 13
13
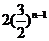 14
14 相交 15
相交 15

16.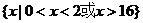
17.解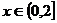 时,
时, , 则
, 则 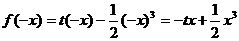
∵函数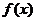 是定义在
是定义在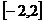 上的奇函数,即
上的奇函数,即
∴ ,即
,即
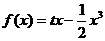 ,又可知
,又可知 
∴函数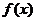 的解析式为
的解析式为
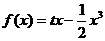 ,
,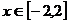
(2) ,∵
,∵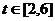 ,
,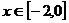 ,∴
,∴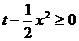
∵ 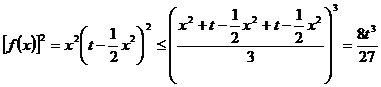
∴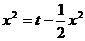 ,即
,即

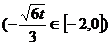 时,
时,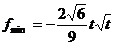

猜想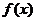 在
在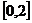 上的单调递增区间为
上的单调递增区间为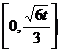

(3)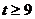 时,任取
时,任取 ,
,
∵
∴ 在
在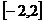 上单调递增,即
上单调递增,即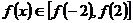 ,即
,即
∵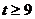 ,∴
,∴ ,∴
,∴
∴当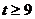 时,函数
时,函数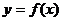 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线 上.
上.
18 (1)解:以O为原点,OA为x轴建立直角坐标系,设A(2,0),
(1)解:以O为原点,OA为x轴建立直角坐标系,设A(2,0),
则椭圆方程为 --------------------------- 2分
--------------------------- 2分
∵O为椭圆中心, ∴由对称性知|OC|=|OB|
又∵ , ∴AC⊥BC
, ∴AC⊥BC
又∵|BC|=2|AC|, ∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1) ----------------- 4分
将C的坐标(1,1)代入椭圆方程得 ,
,
则求得椭圆方程为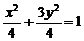 ------------------------------------------ 6分
------------------------------------------ 6分
(2)证:由于∠PCQ的平分线垂直于OA(即垂直于x轴),
不妨设直线PC的斜率为k,则直线QC的斜率为-k,
因此直线PC QC的方程分别为y=k(x-1)+1,y=-k(x-1)+1
QC的方程分别为y=k(x-1)+1,y=-k(x-1)+1
由 得:
得:
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 (*)--------------------------------------------8分
∵点C(1,1)在椭圆上, ∴x=1是方程(*)的一个根,
∴xP•1=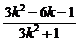 即 xP=
即 xP=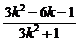
同理xQ= --------------------------------------------------- 10分
--------------------------------------------------- 10分
∴直线PQ的斜率为 ---------12分
---------12分
又∵ ,∴
,∴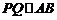 .---------------------------------------------------13分
.---------------------------------------------------13分