
网址:http://www.1010jiajiao.com/paper/timu/5144966.html[举报]
18. (本题12分) 已知向量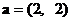 , 向量b与向量a的夹角为
, 向量b与向量a的夹角为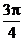 , 且a.b
, 且a.b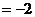 ,
,
(1) 求向量b;
(2) 向量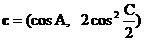 ,
其中A、C是△ABC的内角, 若三角形的三内角A、B、C依次成等差数列, 且与x轴垂直. 试求
,
其中A、C是△ABC的内角, 若三角形的三内角A、B、C依次成等差数列, 且与x轴垂直. 试求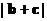 的取值范围.
的取值范围.
高三数学期末综合练习(五)
参考答案及评分标准
一. 选择题(每小题5分,共60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
B |
C |
C |
B |
D |
D |
D |
B |
C |
D |
D |
B |
二. 填空题(每小题4分,共16分)
13. 3或13; 14. 7 ; 15. -1 ; 16. ③ ④ ;
三. 解答题(共74分)
17.(本小题满分12分)
解: (1)由f(0)、f(2)、f(6)成等差数列,
可得2log2(2+m)=log2m+log2(6+m),
即(m+2)2=m(m+6)且m>0,解得m=2. 6分
(2)由f(x)=log2(x+2),可得2f(b)=2log2(b+2)=log2(b+2)2,
f(a)+f(c)=log2(a+2)+log2(c+2)=log2[(a+2)(c+2)], 8分
∵a、b、c成等比数列,∴b2=ac, 9分
又a、b、c是两两不相等的正数,
故(a+2)(c+2)=ac+2(a+c)+4>ac+4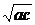 +4=b2+4b+4=(b+2)2, 10分
+4=b2+4b+4=(b+2)2, 10分
∴log2[(a+2)(c+2)]>log2(b+2)2,即f(a)+f(c)>2f(b) 12分
18.(本小题满分12分)
解: 设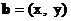 , 则
, 则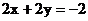 ,……(1分)且
,……(1分)且 .……(3分)
.……(3分)
∴解得 或
或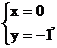
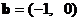 或
或 ……(5分)
……(5分)
(2)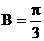 , ……(6分) ∵b⊥x轴, ∴
, ……(6分) ∵b⊥x轴, ∴ ,……(7分)
,……(7分)
∴b+c= ,……(8分)
,……(8分)
∴| b+c |2=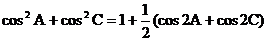
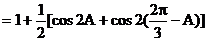
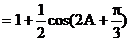 ……(10分)
……(10分)
∵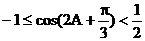 ,
∴
,
∴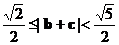 .……(12分)
.……(12分)
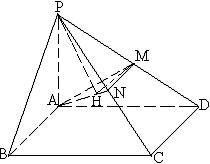 19.(本小题满分12分)
19.(本小题满分12分)
证明: (1) ∵ABCD是正方形, ∴CD⊥AD
∵PA⊥底面ABCD,
∴AD是PD在平面ABCD内的射影,∴CD⊥PD……(2分)
在△PCD中M、N分别是PD、PC的中点, 则MN∥CD,
∴PD⊥MN, 在△PCD中PA=AD=2, M为PD的中点.
∴PD⊥AM, ∴PD⊥平面AMN……(4分)
(2) ∵作MH⊥AN于H, 连接PH, ∵PM⊥平面AMN, ∴PH⊥AN , ∠PHM为二面角P-AN-M的平面角. (10分)
∵PM⊥平面AMN, ∴PM⊥MH. 在Rt△AMN中, MH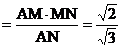
在Rt△PMH中, tan∠PHM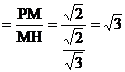 ,……(11分)
,……(11分)
∴∠PHM=60°, 则二面角P-AN-M的大小为60°……(12分)
20.(本小题满分12分)
解: (1)设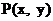 , 因为
, 因为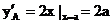 ,……(1分)
,……(1分)
所以过点A的切线方程为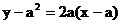 ……(2分)
……(2分)
令 , 则
, 则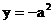 , B点坐标为
, B点坐标为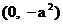 .……(3分)
.……(3分)
又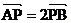 , ∴
, ∴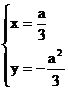 消去a, 得
消去a, 得 ……(6分)
……(6分)
(2)设C到l的距离为d, 则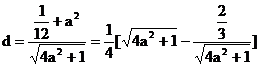 ……(8分)
……(8分)
设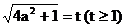 , 则
, 则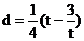 为t的增函数……(10分)
为t的增函数……(10分)
∴ ……(11分)
……(11分)
故C到l的最短距离为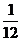 ,
此时l的方程为
,
此时l的方程为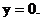 ……(12分)
……(12分)
21.(本小题满分12分)
解: (I)解f(x)=10-f(2m-x)若m=-1,则f(x)关于(-1,5)对称. (1分)
所以a=1,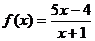 (3分)
(3分)
即 (4分)
(4分)
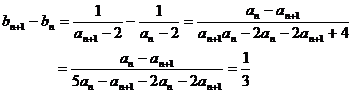
所以{bn}是以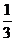 为公差的等差数列. (6分)
为公差的等差数列. (6分)
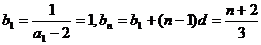 (7分)
(7分)
所以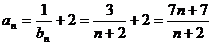 (8分)
(8分)
(II)证明:
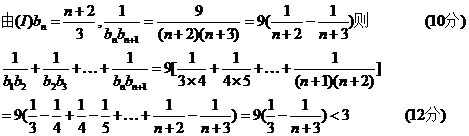
22.(本小题满分14分)
解: (1)设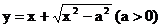 , 则
, 则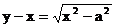 ,
,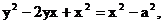
∴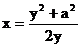 ……(1分)
……(1分)
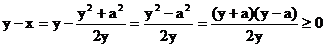 ,
,
∴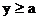 或
或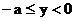 . ∴所求的反函数是:
. ∴所求的反函数是: 
其定义域是:  .……(4分)
.……(4分)
(2) ∵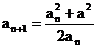 , ∴
, ∴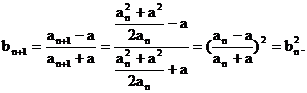 ……(6分)
……(6分)
又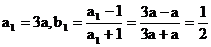 ,
,
∴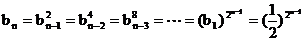 ……(8分)
……(8分)
 ……(9分)
……(9分)
∵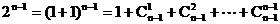 ,
,
则当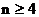 时, 有
时, 有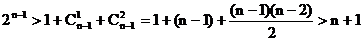 ,……(12分)
,……(12分)
∴ ……(13分)
……(13分)
∴
 ……(14分)
……(14分)