
网址:http://www.1010jiajiao.com/paper/timu/5145069.html[举报]
4. 若一个等差数列的前3项的和为34, 最后3项的和为146, 且所有项的和为390, 则这个数列共有 ( )
A. 13项 B. 12项 C. 11项 D. 10项
高三数学期末综合练习(六)
参考答案及评分标准
一. 选择题(每小题5分,共60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
答案 |
A |
C |
D |
A |
D |
A |
B |
C |
A |
B |
A |
C |
二. 填空题(每小题4分,共16分)
13. (-3, 1) ; 14. 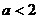 ;
15. ①; 16.
4008
;
;
15. ①; 16.
4008
;
三. 解答题(共74分)
17.(本小题满分12分)
解:
(1)设公差为d, 由已知可得:
 所以等差数列
所以等差数列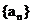 的通项公式为;
的通项公式为;
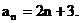 ……(4分)
……(4分)
(2) 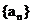 的前n项和为
的前n项和为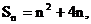 ……(6分)
……(6分)
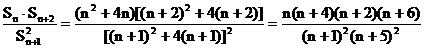
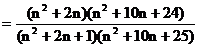 ……(10分)
……(10分)
∵
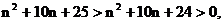
∴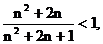
 ∴
∴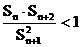 ∴
∴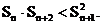 …(12分)
…(12分)
18.(本小题满分12分)
解: (1) . ……(3分)
. ……(3分)
 ,……(6分)
,……(6分)
∵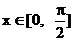 , ∴
, ∴ ……(7分)
……(7分)
(2)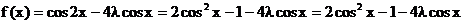
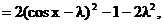 ……(8分)
∵
……(8分)
∵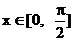 , ∴
, ∴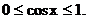
①当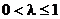 时,
当且仅当
时,
当且仅当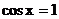 时,
时, 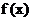 取的最小值
取的最小值 ,
,
由已知得 , 解得
, 解得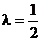 , ……(9分)
, ……(9分)
②当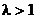 时,
当且仅当
时,
当且仅当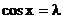 时,
时, 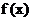 取得最小值
取得最小值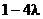 ,
,
由已知得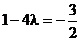 , 解得
, 解得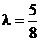 ,这与
,这与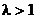 矛盾.……(11分)
矛盾.……(11分)
综上所述,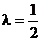 为所求.……(12分
为所求.……(12分
19.(本小题满分12分)
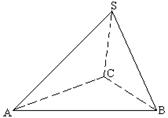
证明: (1)取AC的中点D, 连结SD、BD, ∵SA=SC, D为AC的中点, ∴SD⊥AC.…(2分)
∵AB=BC, D为的AC中点, ∴BD⊥AC. 又SD BD=D, ∴AC⊥面SBD, 又SB
BD=D, ∴AC⊥面SBD, 又SB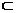 面SBD,∴AC⊥SB. ……(4分)
面SBD,∴AC⊥SB. ……(4分)
(2)过O作OH⊥BC于H, 连SH, 则SH⊥BC. ∴∠SHO为二面角S-BC-A的平面角.……(9分)
∵正△ABC的边长为8, ∴BD= . ∵
. ∵ ,
,
 ∴
∴ 在Rt△OHB中,
在Rt△OHB中, 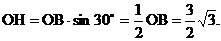 ……(10分)
……(10分)
在Rt△SOH中, 
即二面角S-BC-A的正切值为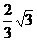 .……(12分)
.……(12分)
20.(本小题满分12分)
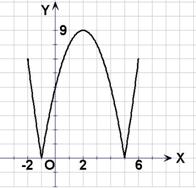 解: (1)
解: (1)
(2)方程 的解分别是
的解分别是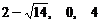 和
和 ,由于
,由于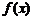 在
在 和
和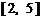 上单调递减,在
上单调递减,在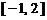 和
和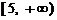 上单调递增,因此
上单调递增,因此
 .
……8分
.
……8分
由 .
.
(3)[解法一] 当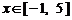 时,
时, .
.
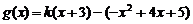
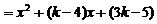
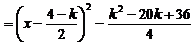 ,
,

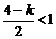 . 又
. 又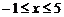 ,
,
① 当 ,即
,即 时,取
时,取 ,
,

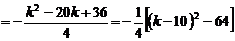 .
.
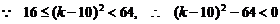 , 则
, 则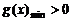 .
.
② 当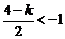 ,即
,即 时,取
时,取 ,
,  =
=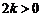 .
.
由 ①、②可知,当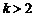 时,
时, ,
,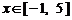 .
.
因此,在区间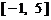 上,
上,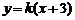 的图像位于函数
的图像位于函数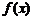 图像的上方.
图像的上方.
[解法二] 当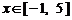 时,
时, .
.
由 得
得 ,
,
令  ,解得
,解得
 或
或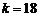 ,
,
在区间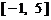 上,当
上,当 时,
时, 的图像与函数
的图像与函数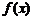 的图像只交于一点
的图像只交于一点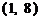 ; 当
; 当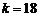 时,
时, 的图像与函数
的图像与函数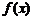 的图像没有交点.
的图像没有交点.
如图可知,由于直线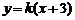 过点
过点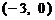 ,当
,当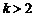 时,直线
时,直线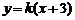 是由直线
是由直线 绕点
绕点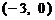 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间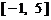 上,
上,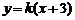 的图像位于函数
的图像位于函数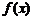 图像的上方.
图像的上方.
21.(本小题满分12分)
解: (1)设椭圆的方程为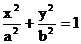 ,
焦距为
,
焦距为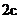 , 则直线l的方程为:
, 则直线l的方程为: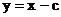 ,
,
代入椭圆方程, 得 , 设点
, 设点 、
、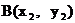 ,
,
则
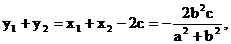 ……(2分)
……(2分)
∵ +
+
 , ∴C点坐标为
, ∴C点坐标为 .
.
 ∵C点在椭圆上, ∴
∵C点在椭圆上, ∴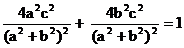 .
.
∴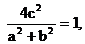 ∴
∴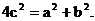 ……(4分)
……(4分)
又 ∴
∴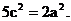
∴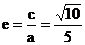 ……(6分)
……(6分)
(2) ∵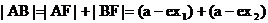
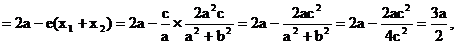 ……(9分)
……(9分)
由已知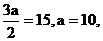 从而
从而 .
.
∴ .故椭圆的方程为:
.故椭圆的方程为:  .……(12分)
.……(12分)
22.(本小题满分14分)
解: (1)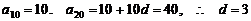 .
…… 3分
.
…… 3分
(2)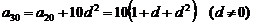 ,
…… 6分
,
…… 6分
 ,
,
当 时,
时,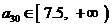 .
…… 10分
.
…… 10分
(3)所给数列可推广为无穷数列 ,其中
,其中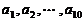 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当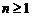 时,数列
时,数列 是公差为
是公差为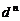 的等差数列.
的等差数列.
研究的问题可以是:试写出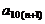 关于
关于 的关系式,并求
的关系式,并求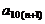 的取值范围.…… 12分
的取值范围.…… 12分
研究的结论可以是:由 ,
,
依次类推可得 
当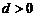 时,
时,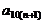 的取值范围为
的取值范围为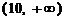 等.
…… 14分
等.
…… 14分