
网址:http://www.1010jiajiao.com/paper/timu/5145167.html[举报]
20..、已知函数f(x)=ax2+bx+1(a,b∈R)
(1)若 f(-1)=0,且对任意实数x均有f(x) ≥0成立,求f(x)表达式
(2)在(1)条件下,当x∈[-2,2]时,S(x)=xf(x)-kx单调递增,求实数k取值范围.
参考答案:
一:BBAAC CDAAC AD
二:13、-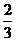 14、2 15、
14、2 15、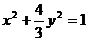 16、3
16、3
三: 17 (本小题满分12分)
(本小题满分12分)
解:由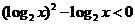 得
得  即1<x<2
即1<x<2
∴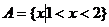 ,
3分
,
3分
由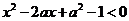 得
得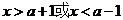
∴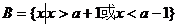 6分
6分
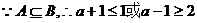 10分
10分
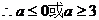 12分
12分
18、(12分)解:(I) ∵|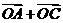 |=
|=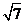 ,即(2+cos
,即(2+cos )2+sin2
)2+sin2 =7 ∴cos
=7 ∴cos =
=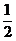
又 ∈(0,
∈(0,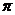 ) ∴
) ∴ =∠AOC=
=∠AOC=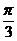
又∠AOB=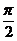 ∴
∴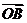 与
与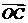 的夹角为
的夹角为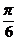 5分
5分
(II)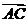 =(cos
=(cos -2,sin
-2,sin ),
), =(cos
=(cos , sin
, sin -2)
-2)
又∵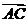 ⊥
⊥ ∴
∴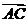 .
. =0
=0
∴cos +sin
+sin =
=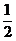 …………………………① 8分
…………………………① 8分
∴2sin cos
cos =-
=-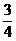 ∵
∵ ∈(0,
∈(0,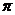 ) ∴
) ∴ ∈(
∈(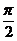 ,
,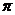 )
)
又由 (cos -sin
-sin )2=1-2sin
)2=1-2sin cos
cos =
=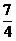 及cos
及cos -sin
-sin <0
<0
是cos -sin
-sin =-
=-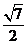 ……………………②
10分
……………………②
10分
由①、②的cos =
=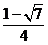 ,sin
,sin =
= ∴tan
∴tan =-
=-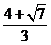 12
12
19(12分)解:(1)∵O、D分别为AC、PC的中点,∴OD∥PA。
又PA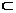 平面PAB,∴OD∥平面PAB。 4分
平面PAB,∴OD∥平面PAB。 4分
(2)∵AB⊥BC,OA=OC,∴OA=OB=OC,又OP⊥平面ABC,
∴PA=PB=PC。取BC中点E,连结PE,则BC⊥平面POE。作OF⊥PE于F,连结DF,则OF⊥平面PBC,∴∠ODF是OD与平面PBC所成的角。
又OD∥PA,∴PA与平面PBC所成的角的大小等于∠ODF。
在直角⊿ODF中,sin∠ODF=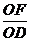 =
=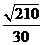
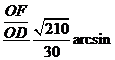 ∴PA与平面PBC所成的角为
∴PA与平面PBC所成的角为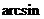
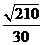 。 8分
。 8分
(3)
由(2)知,OP⊥平面ABC, ∴F是O在平面ABC内的射影。
∴F是O在平面ABC内的射影。
∵D是PC的中点,若点F是⊿PBC的重心,则B、F、D三点共线,∴直线OB在平面PBC内的射影为直线BD。
∵OB⊥PC, ∴PC⊥BD, PB=PC,即m=1.
∴PC⊥BD, PB=PC,即m=1.
反之,当m=1时,三棱锥O-PBC为正三棱锥,∴O在平面PBC内的射影为⊿PBC的重心。 12分
解法2:建立空间直角坐标系亦同样得分。
20(12分)解:(1)∵任意,x∈R,均有f(x)≥0,而f(-1)=0
∴a>0,且f(x)=a(x+1)2
从而ax2+bx+1=a(x+1)2得:b=2a且a=1
∴f(x)=x2+2x+1 6分
(2)依题意,当x∈[-2,2]时,g(x)=x3+2x2+x-kx为增函数
∴g(x)=3x2+4x+1-k≥0
即k≤3(x+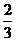 )2-
)2-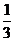
∵3(x+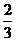 )2-
)2-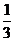 ≥-
≥-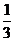 在[-2,2]恒成立.
在[-2,2]恒成立.
∴k≤-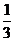 12分
12分
21、(12分)(1)当n≥2时,Sn=n-an,Sn-1=(n-1)-an-1
∴an=Sn-Sn-1=1+an-1-an 2
∴2(an-1)=an-1-1 即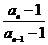 =
=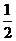 而a1=1-S1
而a1=1-S1 a1=
a1=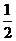 4
4
∴数列{an-1}是以a1-1=-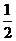 为首项,以
为首项,以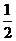 为公比的等比数列
为公比的等比数列
∴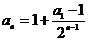 =1-
=1-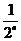 ,从而bn+1=an+1-an=
,从而bn+1=an+1-an=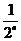 -
-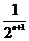 =
=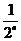 6 分
6 分
(2)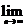 an=
an=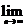 (1-
(1-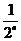 )=1
8 分
)=1
8 分
(3)Cn=2n-1 ∴C1+C2+…+Cn
=(2+22+…+2n)-n
=2n+1-2-n 10分
∴2n+1-2-n<400 故n=7 12 分
22、(14分)解:(1) 设点M的坐标为 (x, y),点P的坐标为 (x1,0),点Q的坐标为
(0,y2) (x1≠0),则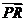 =(-x1,-3),
=(-x1,-3),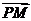 =(x-x1,y),
=(x-x1,y),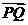 =(-x1,y2)
=(-x1,y2)
∵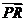 ⊥
⊥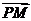 ∴
∴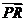 .
.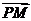 =0 ∴-x1(x-x1)-3y=0
=0 ∴-x1(x-x1)-3y=0
即x12-x1x-3y=0 由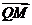 =2
=2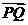 得
得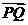 =
=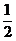
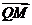
∴x1=-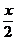 代入上式的y=
代入上式的y=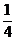 x2
(x≠0)
6分
x2
(x≠0)
6分
(2) 设切点为 (x0, y0) ∵y1=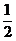 x ∴切线
x ∴切线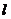 0=
0=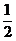 x0=tan
x0=tan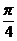 =1
=1
∴x0=2 切点为 (2,1) ∴切线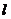 0的方程为x-y-1=0 8分
0的方程为x-y-1=0 8分
(3) ∵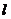 0的切线方程为x-y-1=0 ∴G (0, -1)
0的切线方程为x-y-1=0 ∴G (0, -1)
设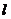 的斜率为k ∴
的斜率为k ∴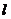 的方程为y=kx-1
的方程为y=kx-1
由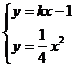 的x2-4k
的x2-4k +4=0…………①
+4=0…………①
设A(x1, y1),B(x2, y2),则x1, x2是方程①的两根
∴△=16k2-16 >0 ∴k2>1 10分
∵∠ADB为钝角 ∴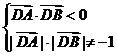
而|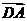 |=(x1;y1-1),
|=(x1;y1-1),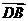 =(x2,
y2-1)
=(x2,
y2-1)
∴x1.x2+(y1-1) (y2-1)<0 ∴x1x2+(k x1-2) (kx2-2) <0
∴x1x2+k2 x1x2-2k(x1+x2)+4<0即k2-2>0 ∴k<-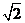 或k>
或k>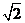 14分
14分