
网址:http://www.1010jiajiao.com/paper/timu/5145219.html[举报]
4. 函数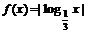 的单调递增区是
的单调递增区是
A.  B.(0,+∞)
C.
B.(0,+∞)
C.  D.
D.
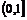
参考答案及评分标准
一、选择题:本大题共12小题,每小题5分,共60分
DACAB BCDBC BA
二、填空题:本大题共4小题,每小题4分,共16分
13、2 14、样本 15、8 16、①③
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。
17、解:由3+2x-x2>0,有-1<x<3,………………………………2分
 .
.
 C1
C1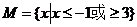 .…………………………………………4分
.…………………………………………4分
由|x-a|≤1,有-1≤x-a≤1,即a-1≤x≤a+1,
 N={x|a-1≤x≤a+1}.…………………………6分
N={x|a-1≤x≤a+1}.…………………………6分
 (C IM)∩
N=
(C IM)∩
N= ,
,
 a-1>-1且a+1<3.…………………………………9分
a-1>-1且a+1<3.…………………………………9分
即0<a<2.
 a
a Z;
Z;
 a=1.…………………………11分
a=1.…………………………11分
 N={x|0≤x≤2}.
N={x|0≤x≤2}.
 M∩N={x|0≤x≤2}……………………12分
M∩N={x|0≤x≤2}……………………12分
18、解:如图,设地基的长和宽分别为xm、ym,其中0<x<40,0<y<30。
|
 面积S=xy。
面积S=xy。
|
|

 ,
,





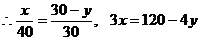 .………………5分
.………………5分
|
|
|
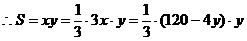
|
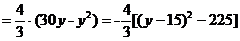 .……………………9分
.……………………9分
 ,
,
 当y=15时(此时x=20),Smax=300.
当y=15时(此时x=20),Smax=300.
所以这块地基能达到的面积最大是300m2,面积最大时地基的长和宽分别是20m和15m. …………12分
19、解 f(x)在定义域(-1,1)内可导并满足
f(x)在定义域(-1,1)内可导并满足 ,
,
 f(x)在(-1,1)内是减函数, ………………3分
f(x)在(-1,1)内是减函数, ………………3分
 由f(1-m)+f(1-m2)>0有f(1-m)>-f(1-m2)
由f(1-m)+f(1-m2)>0有f(1-m)>-f(1-m2)
 由f(x)是奇函数得f(1-m)>f(m2-1). ……………………6分
由f(x)是奇函数得f(1-m)>f(m2-1). ……………………6分
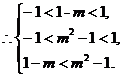 ………………10分
………………10分
 .
.
 原不等式的解集为(1,
原不等式的解集为(1,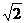 ). ………………12分
). ………………12分
20、(1)解: f1(x)的值域为[-2, +∞),
f1(x)的值域为[-2, +∞), f1(x)
f1(x)
 A. …………2分
A. …………2分
对于f2(x),定义域为[0,+∞),满足条件①.
而由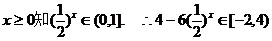 ,满足条件②.
,满足条件②.
又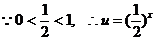 在[0,+∞)上是减函数.
在[0,+∞)上是减函数.
 f2(x)在[0,+∞)上是增函数,满足条件③.
f2(x)在[0,+∞)上是增函数,满足条件③.
 f2(x)属于集合A. ……………………6分
f2(x)属于集合A. ……………………6分
(2)由(1)知, f2(x)属于集合A.
 原不等式为
原不等式为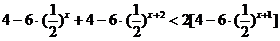 .………………8分
.………………8分
整理为: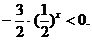 ……………………10分
……………………10分
 对任意
对任意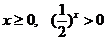 ,
,
 原不等式对任意x
原不等式对任意x 0总成立. ………………12分
0总成立. ………………12分
21、解:(1) f(x)对任意x,y都有f (x. y)=y. f (x)+x.
f (y),
f(x)对任意x,y都有f (x. y)=y. f (x)+x.
f (y),
 令x=y=1时,有f (1.1)=1.f (1)+1.
f (1),
令x=y=1时,有f (1.1)=1.f (1)+1.
f (1),
 f (1)=0. ……………………………………………………2分
f (1)=0. ……………………………………………………2分
 令x=y=-1时,有f [(-1).(-1)]=(-1).f (-1)+(-1).f
(-1),
令x=y=-1时,有f [(-1).(-1)]=(-1).f (-1)+(-1).f
(-1),
 f (-1)=0. ……………………………………………………5分
f (-1)=0. ……………………………………………………5分
(2) f(x)对任意x,y都有f (x.y)=y.f (x)+x.f
(y),
f(x)对任意x,y都有f (x.y)=y.f (x)+x.f
(y),
 令x=t,y=-1,有f (-t)=-f
(t)+t.f (-1),
令x=t,y=-1,有f (-t)=-f
(t)+t.f (-1),
将f (-1)=0代入得f (-t)= -f (t),
 函数f(x)是(-∞,+∞)上的奇函数. ……………………9分
函数f(x)是(-∞,+∞)上的奇函数. ……………………9分
(3)由已知有f (a-2.a2)=a2.f (a-2)+a-2.f (a2),
即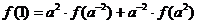 ,
,
由(1)知f (1)=0,

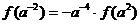 ,
,
而

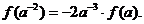
即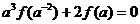 . ……………………12分
. ……………………12分
22、解:(1) , ………………2分
, ………………2分
 由x=1是原方程的一个极值点有
由x=1是原方程的一个极值点有 .
.
 3-2n+3m+3=0.
3-2n+3m+3=0.
 3m-2n+6=0 …………………………5分
3m-2n+6=0 …………………………5分
(2)由(1)有
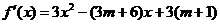
=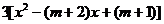
=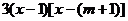 .
.
由 ,……………………8分
,……………………8分
当m+1<1即m<0时,由下表
|
x |
(-∞,m+1) |
m+1 |
(m+1,1) |
1 |
(1,+∞) |
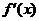 |
+ |
0 |
- |
0 |
+ |
|
f (x) |
↗ |
f (m+1) |
↘ |
3m+5 |
↗ |
 原函数的单调递增区间为(-∞,m+1),(1,+∞). ……………………11分
原函数的单调递增区间为(-∞,m+1),(1,+∞). ……………………11分
当m+1>1即m>0时,下表有
|
x |
(-∞,1) |
1 |
(1,m+1) |
m+1 |
(m+1,+∞) |
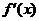 |
+ |
0 |
- |
0 |
+ |
|
f (x) |
↗ |
3m+5 |
↘ |
f (m+1) |
↗ |
 原函数的单调递增区间为(-∞,1),(m+1,+∞).
原函数的单调递增区间为(-∞,1),(m+1,+∞).
 综上所述,当m<0时,原函数的单调递增区间为(-∞,m+1),(1,+∞);当m>0时,原函数的单调递增区间为(-∞,1),(m+1,+∞). ……………………14分
综上所述,当m<0时,原函数的单调递增区间为(-∞,m+1),(1,+∞);当m>0时,原函数的单调递增区间为(-∞,1),(m+1,+∞). ……………………14分