19．解：⑴解法(一)(1)以D为原点，DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系0－xyz，则D(0，0，0)，A(2，0，0)，C(0，2，0)，B(2，2，0)，
A1(2，0，4)，D1(0，0，4)，C1(0，2，4)，B1(2，2，4)，
设E(0，2，t)，则∵
且
(2)设A1C∩平面BDE=K，
设A1C∩平面BDE=K，
…①
同理有…②
由①，②联立解得
即所求角的正弦值是
解法(二)(1)证明：连AC交BD于点O，由正四棱柱性质可知AA1⊥底面ABCD，AC⊥BD，∴A1C⊥BD
又∵A1B⊥侧面BC1且B1C⊥BE， ∴A1C⊥BE，
∵BD∩BE=B， ∴A1C⊥平面BDE
(2)解：设A1C交平面BDE于点K，连BK，
则∠A1BK为A1B与平面BDE所成的角，
∵在侧面BC1中BE⊥B1C，∴△BCE∽△B1BC，
连结OE，则OE为平面ACC1A1与平面DBE的交线，
即为A1B与平面BDE所成的角的正弦值.
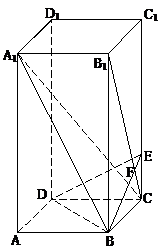(本题12分)如图，已知正四棱柱ABCD-A1B1C1D1中，底面边长AB=2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F.