
网址:http://www.1010jiajiao.com/paper/timu/5145489.html[举报]
4. 等差数列{an}中,已知a1=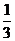 ,a2+a5=4,an=33,则n为( )
,a2+a5=4,an=33,则n为( )
A.50 B.49 C.48 D.47
高三单元试题之三:数列参考答案
一、1.D 2.C 3.B 4.A 5.A 6.D 7.C 8.A 9.C 10.D 11.B 12.C
二、13.27 14.2 15.9 16.a,-a,a,-a,…(a≠0),r与s同为奇数或偶数
三、17.解:⑴∵a1=23,a6>0,a7<0,∴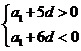

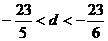
∵d为整数,∴d=-4。
⑵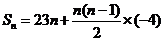 =23
=23 =-2
=-2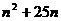 =-
=-
∴当 时,Sn最大=78。
时,Sn最大=78。
⑶Sn=-2n2+25n>0得0 ,∴n最大为12。
,∴n最大为12。
18.解:⑴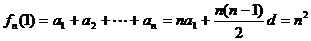
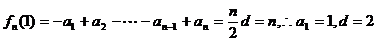 ,∴an=2n-1(n∈N+)
,∴an=2n-1(n∈N+)
⑵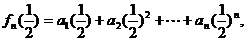 ∴通过差比数列求和可得:
∴通过差比数列求和可得:
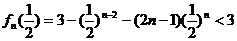 ,又可证
,又可证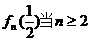 时为单调递增函数。
时为单调递增函数。
∴ ,综上可证
,综上可证 。
。
19.解:(1)该市逐年投入的电力型公交车的数量组成等比数列{an},其中a1=128,q=1.5,
则在2010年应该投入的电力型公交车为a7=a1q6=128×1.56=1458(辆)。
(2)记Sn=a1+a2+…+an,依据题意,得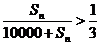 。于是Sn=
。于是Sn= >5000(辆),即1.5n>
>5000(辆),即1.5n>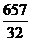 ,则有n≈7.5,因此n≥8。
,则有n≈7.5,因此n≥8。
∴到2011年底,电力型公交车的数量开始超过该市公交车总量的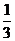 。
。
20.解:⑴令n=1,S1=2a1-3。∴a1 =3 ,又Sn+1=2an+1-3(n+1), Sn=2an-3n,两式相减得,
an+1 =2an+1-2an-3,则an+1 =2an+3
⑵按照定理:A=2,B=3,∴{ an+3}是公比为2的等比数列。
则an+3=(a1+3).2n-1=6.2n-1,∴an =6.2n-1-3 。
⑶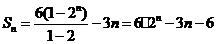 。
。
21.解:⑴设2004年底沙漠面积为b1,经过n年治理后沙漠面积为bn+1。则an+bn=1。
依题意,an+1由两部分组成,一部分是原有的绿洲面积减去沙漠化后剩下的面积,
an-4%an=96%an,另一部分是新植树绿洲化的面积16%bn,于是
an+1=96%an+16%bn =96%an
+16%(1-an)=80% an +16%=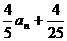 。
。
⑵由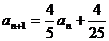 两边减去
两边减去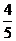 得
得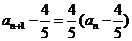 ,∴
,∴ 是以
是以 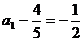 为首项,
为首项,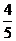 为公比的等比数列。
为公比的等比数列。
⑶由⑵可知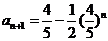 ,依题意
,依题意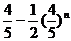 >60%,即
>60%,即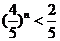 ,两边取对数得
,两边取对数得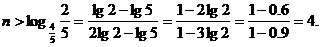
故至少需要5年才能达到目标。
22.⑴P1(-1,0),an=-1+(n-1)×1=n-2,bn=2(n-2)+2=2n-2
⑵f(n)= ,假设存在符合条件的k
,假设存在符合条件的k
①若k为偶数,则k+5为奇数,有f(k+5)=k+3,f(k)=2k-2,
如果f(k+5)=2f(k)-2,则k+3=4k-6 k=3与k为偶数矛盾。
k=3与k为偶数矛盾。
②若k为奇数,则k+5为偶数,有f(k+5)=2k+8,f(k)=k-2,
如果f(k+5)=2f(k)-2,则2k+8=2k-6,这样的k也不存在。
故不存在符合条件的k。
⑶∵Pn(n-2,2n-2),∴|P1Pn|=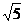 (n-1),(n≥2)
(n-1),(n≥2)
∴
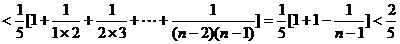 。
。